현실에서 유용한 Bitwise 연산 및 활용 모음

0. Index

들어가며

필수 지식 확인

2.1. (1 << n): n번째 비트 켜기

2.2. (1 << n) - 1: n개의 비트 모두 켜기

유용한 트릭 소개

3.1. 정수의 2의 지수승 여부 확인하기

3.2. 2진수에서 1 비트의 개수 구하기

3.3. Boolean값 Toggle하기

집합론과 비트의 만남

4.1. 2진수의 집합 표현

4.2. 차집합: 비트 연산으로 구현하기

4.3. 그게 최선입니까? 확실해요?

마치며

자료 출처

1. 들어가며

프로그래밍을 처음 배운다고 하자. 요즘 입문용으로는 파이썬을 많이 쓰니 파이썬을 배우게 됐다. 변수와 반복문, 조건문 등을 거쳐 반드시 연산자에 대해 살펴보게 된다. +, -, \*, // 등의 사칙연산용 연산자나 조건연산자 등과 함께 비트 연산자도 공부하게 된다. 그런데 내 경험상 프로그래밍을 처음 공부할 때 비트는 지나치게 어려운 개념이다. 그리고 ‘저걸 배워서 어디에 쓸까’하는 생각이 강하게 들기 때문에 대충 공부하고 넘어간 기억이 있다.

하지만 프로그래밍 경험이 늘면서, 특히 알고리즘을 공부하면서 때로는 비트 단위 연산이 유용하다는 것을 알게 되었다. 그래서 공부하기 시작했으며 이제는 기본적이며 유용한 수준까지는 쓸 수 있게 되었다. 오늘 포스트는 내가 프로그래밍을 하면서 유용하게 썼던 비트 단위 연산과 그 활용을 살펴보려고 한다. 이 포스트는 개인적으로 기대가 된다. 비트 연산이 생각보다 꽤 유용하고 주제 자체가 재미있어서, 포스트를 준비할 때 내용을 어떻게 풀어가야할지 머릿속에서 그림이 깨끗하게 그려진 적은 오랜만이기 때문이다.

시작하기에 앞서 짚고 넘어간다. 일단 이 포스트는 독자분들이 기본적인 비트 연산자와 그 의미는 파악하고 있다고 가정한다. 이번 포스트에서는 >>, ~ 등의 비트 연산자가 쓰일 예정인데 그 의미를 구구절절 설명하지는 않는다. 하지만 포스트 전체 내용을 관철하는 필수 지식은 처음에 조금 다루기는 한다.

또 이 포스트에서 다루는 비트 연산의 수준은 내가 이해하는 범위로, 대략 초급과 중급 사이의 난이도라고 생각하면 된다. 비트로 할 수 있는 일은 생각보다 더 무궁무진하다. 하지만 난 다 알지 못한다. 만약 이 내용이 너무 쉬워서 쓴웃음이 나오는 분들은『해커의 기쁨』, 이 책을 공부하시면 된단다. 아주 그냥 비트로 쌈싸먹고 다 해먹는단다. 나중에 나도 공부해보면 재밌겠지만 지금은 계획에 없다.

아, 마지막으로 비트 연산자를 활용한 기능의 구현은 파이썬으로 했다. 하지만 비트 연산자 기호는 다른 많은 고급언어에서 동일한 것으로 알고 있기 때문에 의미만 읽을 수 있으면 사용하는 언어로 구현가능할 것이다.

시작합니다.

2. 필수 지식 확인

먼저 <<과 관련된 연산의 의미를 파악하고 넘어가려고 한다. 이 연산자는 다 아시다시피 왼쪽 연산자의 비트를 오른쪽 연산자 수만큼 왼쪽으로 당기는 것을 의미한다. 이 연산은 특정한 방법으로 사용하면 인간에게 유용한 특정 의미로 해석될 수 있다. 소개할 두 식은 매우 비슷하지만 의미는 완전히 다르기 때문에 잘 살펴보자. 이 내용은 중요해서 처음에는 그냥 외워도 좋다. 이번 장의 나머지 부분은 사실상 이 부분의 활용이라고 봐도 된다.

2.1. `(1 << n)`: n번째 비트 켜기

n이 0 이상의 정수일 때, ’(1 << n)은 n번째 비트를 켠다’는 의미를 갖고 있다. 순수한 정수 1은 비트의 세계에서는 ‘0번째 비트가 켜져 있다’는 의미와 동일하다. (1 << n)은 0번째 켜져 있는 비트를 n만큼 왼쪽으로 옮겼기 때문에 결과적으로 ‘n번째 비트를 켠다’는 의미와 동일해진다.

정말 그런지 간단한 예를 들어서 확인해보자.

def nth_bit_on(n):
    return (1 << n)

print(bin(nth_bit_on(1)))
print(bin(nth_bit_on(2)))
print(bin(nth_bit_on(3)))
print(bin(nth_bit_on(4)))

0b10
0b100
0b1000
0b10000

파이썬의 bin 함수는 인자가 하나일 때는 주어진 정수를 2진수 형태의 문자열로 반환한다. 앞에 붙은 ‘0b’는 식별자라고 생각하면 된다.

예제에서는 1, 2, 3, 4번째 비트를 켠 수를 반환하라고 했는데 확인 결과 정확히 그 비트를 켜서 반환함을 알 수 있다. 혹시나 착각하지 말자. 비트를 셀 때 0번째를 포함해야 한다. 그래서 4번째 비트를 켠 수는 \(1000_{(2)}\)가 아닌 \(10000_{(2)}\)이 된다. 오른쪽에서 순서상 5번째 값이 켜진 것이다. 이는 10진수도 마찬가지다.

이를 활용한 간단한 예제를 만들어보자. 어떤 정수의 nth번째 비트가 켜져 있는지, 꺼져 있는지 확인해야 한다고 하자. 함수는 다음과 같이 한 줄로 작성할 수 있다.

def get_nth_bit(n, nth):
    return 1 if n & (1 << nth) else 0


print('10진수 100을 2진수로 변환한 값:', bin(100))
print(get_nth_bit(100, 2))
print(get_nth_bit(100, 3))


10진수 100을 2진수로 변환한 값: 0b1100100
1
0

정수 n의 nth번째 비트의 on/off 여부를 반환하는 get_nth_bit 함수를 정의했다. 이 식의 핵심은 n & (1 << nth)이다. ‘(1 << nth)은 nth번째 비트를 켠다’라고 했다. 이를 활용해서 확인할 n과, nth번째 비트를 켠 수를 & 연산하면 답이 0일 시에는 0, 아닐 시에는 다른 값이 나올 것이다.

이때 왜 삼항연산자를 쓰는지 궁금할 수 있다. 어차피 0과 1을 반환하면 이 둘은 파이썬에서 False과 True로 취급되기 때문에 그냥 반환하면 되지 않느냐고 말이다.

def get_nth_bit(n, nth):
    return n & (1 << nth)

얼핏 보기에는 문제가 없는 것 같다. 근데 이는 디버깅이 매우 어려운 치명적인 실수로 조심해야 한다. 만약 비트가 꺼져 있다면 0이 반환된다. 근데 0이 아니라면, 다시 말해 해당 nth 번째 비트가 켜져 있다면 반환되는 값은 0이 아니라 nth번째 비트가 켜진 정수다. 이 값은 nth이 2, 3, 4임에 따라 4, 8, 16 등의 값이 된다. 그래서 0이 아니면 반드시 1을 반환하도록 삼항연산자를 쓸 수밖에 없다.

이는 다른 비트 연산에도 적용되는 부분이니 조심하도록 하자.

2.2. `(1 << n) - 1`: n개의 비트 모두 켜기

2절의 제목을 보고 기시감이 느껴진다면 그건 당연한 것이다. 2절의 식은 1절의 식과 거의 유사하다. 단지 식에서 1을 빼고 있을 뿐이다. 하지만 의미는 완전히 달라진다. ’(1 << n) - 1은 n개의 비트를 모두 켠다’는 의미를 갖고 있다. 4개의 비트를 모두 켠 2진수는 \(1111_{(2)}(15)\)이고 8개의 비트를 모두 켠 2진수는 \(11111111_{(2)}(255)\)이다. 앞선 절에서는 n번째 비트를 켜는데 그때는 0번째를 고려해야 해서 헷갈릴 수도 있지만 2장의 내용은 단순히 ‘주어진 개수만큼 비트를 켠다’기 때문에 더 직관적으로 와닿는다.

일단 정말 그런지 확인해보자.

print(bin((1 << 1) - 1))
print(bin((1 << 2) - 1))
print(bin((1 << 3) - 1))
print(bin((1 << 4) - 1))
print(bin((1 << 8) - 1))


0b1
0b11
0b111
0b1111
0b11111111

정말 정확하게 값이 나온다.

저 식을 단순히 외우지 말고 쉽게 이해할 수 있는 방법이 있을까? 당연히 있다. 우리가 매일 하는 10진수 연산을 이 식과 연관시키면 된다. 우리 모두, ‘\(10000 - 1 = 9999\)‘라는 것을 안다. 근데 이 식은 이번 절의 식과 매우 비슷하다는 것을 느낄 수 있다. 10진수 식에서 10000에서 1을 빼면 오른쪽부터 시작해서 0인 부분은 9(10-1)로 치환되고 0이 아닌 부분까지 진행하며 최종적으로 0이 아닌 처음 자리값을 1 낮춘다. 2번 식은 저것과 똑같다. (1 << n)은 n번째 비트가 1이고 그 아랫자리값은 모두 0이기 때문에 오른쪽에서부터 0인 부분은 1(2-1)로 모두 바꾸고 0이 아닌 첫 부분(n번재 비트) 자리값을 0으로 낮춘 것이다. 이렇게 이해하면 2번 절의 내용이 매우 쉽게 이해가 된다.

이를 활용한 간단한 예제를 만들어보자. 매우 간단한 비트마스킹(bitmasking)을 해보자. 간단히 말해 비트마스크는 어떤 숫자에 마스크라고 불리는 비트값을 비트 연산해서 숫자의 특정 비트 구간값을 변경시키거나, 그 값을 추출하는 등의 행위를 말한다. 예를 들어서 \(1001 \text{ } 1011 \text{ } 1111 \text{ } 0101_{(2)}(39925)\)라는 2진수에서 오른쪽 두 번째 구간의 4개의 비트값을 빼오고 싶다면 특정 마스크와 이 수를 비트마스킹해서 추출할 수 있다.

이런 짓을 왜 해야할까? 많은 유용한 예가 있겠지만 여기서는 네트워크 IP 패킷을 예로 살펴 보자.

IP packet's header image

위 그림은 IP 패킷의 헤더 부분의 구성 데이터이다. IP 패킷은 TCP/IP 네트워크 모델의 IP 프로토콜에서 주고 받는 메시지 단위로 IP 패킷은 호스트, 즉 컴퓨터, 핸드폰 등 네트워크 인터페이스를 구별하는 역할을 하며 다시 헤더와 데이터로 나뉜다. 데이터는 실제 전송하는 데이터고 헤더는 전달해야 할 데이터보다는 IP 패킷에 대한 메타데이터를 담고 있다. 그림에서 IP 헤더는 출발지, 목적지 IP 주소, 버전, 길이, 체크섬 등 IP 패킷의 전달과 해석에 대한 정보를 담고 있는 것을 확인할 수 있다.

여기서 중요한 건 그림 바로 위의 숫자들인데 헤더의 각 부분은 자신을 표현하는 값을 갖고 있으며 그 범위는 비트 단위로 표현된다. 예를 들면, 헤더의 첫 4비트는 IP Version을 기록하는 데 사용하고, 4번째 행은 출발지 IP로 이를 표현하기 위해 32비트를 사용한다. 한 행이 32비트, 4바이트로 따로 옵션이 붙지 않을 때 IP 헤더의 기본 크기는 4 X 5, 즉 20바이트가 된다.(그림에서 6번째 행은 생략될 수도 있다.)

컴퓨터 입장에서 이렇게 배달된 IP 헤더에서 이 패킷이 IPv4 버전인지, IPv6 버전인지를 확인해야 한다고 하자. 이때 비트마스킹이 필요해진다. 헤더는 현재 20바이트의 비트 데이터 형태인데 이 값의 처음 4비트만 추출하는 비트마스킹을 적용하면 전체 헤더에서 버전 정보만 추출할 수 있다!

이는 실제 라우터와 다른 컴퓨터들이 지금도 하고 있는 작업으로 비트마스킹의 매우 중요한 예시 중 하나일 뿐이다.

위의 예를 쉽게 바꿔서 주어진 수의 오른쪽 끝에서 n개의 비트값을 추출하는 기능을 만들자.

from random import randint

def get_trailing_bits(n, count):
    return n & ((1 << count) - 1)

N = randint(1, 2 ** 32)
last_4_bits = get_trailing_bits(N, 4)

print('N은', N, ', 2진수로는', bin(N), '입니다.')
print('이때 N의 마지막 4개의 비트는', '{:04b}'.format(last_4_bits), '입니다.')

N은 98760010 , 2진수로는 0b101111000101111010101001010 입니다.
이때 N의 마지막 4개의 비트는 1010 입니다.

random 내장 모듈의 randint 함수를 써서 테스트할 정수를 정한다. 이 함수는 값을 선택할 범위를 의미하는 두 값을 갖는데 특징은 마지막 값도 포함한다.(inclusive) 배열 슬라이싱에서 범위의 마지막 값이 무시되는 것과는 대조적이다.

get_trailing_bits 함수는 주어진 수 n 에서 count 개만큼의 마지막 비트를 추출한다. 결과는 정확하게 출력된다. 만약 n 의 2진수 표현의 길이가 4가 못되면 빈 부분은 0으로 채워서 표현한다.

정말 쉬운 비트마스킹 예제로 이보다 더 심화해서 중간의 어떤 범위의 비트를 확인하는 등의 보다 복잡한 마스킹은 이 포스트의 범위를 넘어가기에 다루지 않는다.

정리하면 (1 << n)은 ‘n번째 비트를 켠다’는 의미이고 (1 << n) - 1은 ‘n개의 비트를 모두 켠다’가 된다. 이에 대한 이해를 바탕으로 다음 내용을 공부하자.

3. 유용한 트릭 소개

이제 실전에서 유용한 몇 가지 비트 연산 트릭을 살펴보자. 여기서 말하는 ‘유용’은 알고리즘 문제에서 쓸모 있거나, 실제 프로그램 개발에서 써먹을 수 있는 것을 의미한다. 이 장의 내용들은 향후에 재미있고 유용한 비트 연산을 찾을 때마다 내용을 추가할 수 있도록 하겠다.

3.1. 정수의 2의 지수승 여부 확인하기

첫 번째 해결할 문제는 간단하다. 임의의 정수가 2의 지수승인지, 다시 말해 \(2^k\)의 꼴로 표현될 수 있는지(k는 0 이상의 정수)를 판단하는 기능을 만들자. 이 기능은 1, 2, 4, 8, 16 등의 수들에서는 True를 반환하고, 3, 15, 22, 35 등의 수들에서는 False을 반환해야 한다.

코드는 다음과 같다.

def is_exp_binary(n):
    return n & (n - 1) == 0

놀랍게도 단 한 줄로 정의된다. 맞는지 확인해보자.

print(1, is_exp_binary(2 ** 0))
print(2, is_exp_binary(2 ** 1))
print(4, is_exp_binary(2 ** 2))
print(1024, is_exp_binary(2 ** 10))

print(3, is_exp_binary(3))
print(15, is_exp_binary(15))
print(101, is_exp_binary(101))
print(1000, is_exp_binary(1000))

1 True
2 True
4 True
1024 True
3 False
15 False
101 False
1000 False 

결과는 정확하게 의도한 대로 나온다. 그러면 왜 이런 결과가 나올까? 임의의 정수 n이 \(2^k\)형태의 수라면(k는 0 이상의 정수), 이 수는 앞선 장에서의 (1 << k)와 정확히 같다. 이 수는 맨 처음 비트는 1이고 그 아랫자리 비트는 모두 0이다. n이 \(1000_{(2)}\)(8)이라고 하자. 이때 ‘n - 1’은 첫 번째 비트는 끄고 그 아랫자리 비트는 모두 1로 만든다. 즉 ‘n - 1’은 \(111_{(2)}\)(7)이 되고, 이 두 수에 & 연산을 하면 반드시 0이 나온다.

\[ \begin{equation} \frac{ \begin{array}[b]{r} 1000_2 \\ \text{&} 111_2 \end{array} }{ 0000_2 } \end{equation} \]

그래서 두 수에 & 연산한 결과가 0이면 n이 2의 지수승인 것을 알 수 있다. 그러면 n이 2의 지수승이 아니면 0이 아닌 값이 나오는가? 실제로 그렇다. 몇 번만 테스트해보라.

이 트릭은 실제 개발에서 쓴다기보다는 알고리즘 문제에서 제출할만하다. 방법 자체는 매우 세련됐는데 문제가 너무 쉬워서 Codewars에서 한 7급이나 6급이면 괜찮을 것 같다.

3.2. 2진수에서 1 비트의 개수 구하기

다음 문제도 초보적인 알고리즘 문제다. 어떤 0 이상의 정수 n을 2진수화했을 때, 켜진(값이 1인) 비트의 개수는 몇 개일까? 이 문제를 푸는 방법은 다양한데 가장 무난한 방법은 n을 while 반복문 안에서 2로 나눠가면서 나머지가 있을 때마다 개수를 1씩 늘려서 최종적인 개수를 반환하는 방법이다.

이렇게 수를 2로 나눠가는 방식을 재귀함수로 한 줄로 짤 수도 있다. 파이썬으로 짜면 다음과 같다.

def count_bit(n):
    return n % 2 + count_bit(n // 2) if n >= 2 else n

print('1000은 2진수로', bin(1000), '이고, 1의 개수는', count_bit(1000), '개입니다.')

1000은 2진수로 0b1111101000 이고, 1의 개수는 6 개입니다.

정확하게 동작한다. count_bit 함수는 정수를 2로 나눠가면서 그 값을 재귀호출한다. 1의 개수를 세는 코드는 ‘n % 2’로서 나머지가 1일 때는 비트가 켜진 것이고, 0일 때는 비트가 꺼진 것이다. 그리고 재귀함수는 언제나 기저사례가 필요한데 n이 2보다 작으면 1이나 0일 것이기 때문에 그대로 반환한다.

이 코드 자체도 누군가에게는 어썸할 수도 있다. 나도 꽤나 괜찮은 방법이라고 생각한다. 하지만 굳이 지적하자면 단점이 몇 가지 있다.

직관적이지 않다.
- 우리는 2진수 표현에서 켜져 있는 비트의 개수를 센다. 하지만 이 함수는 비트 연산자가 쓰지 않기 때문에 ‘각 비트 자릿수의 0/1 여부를 확인한다’는 개념이 직관적으로 보이지 않는다.
상대적으로 느리다.
- 사칙연산에서 더하기, 빼기, 곱하기에 비해 나누기(/, //), 나머지 연산(%)은 상대적으로 느리다. 비트 연산자는 일반적으로 매우 빠르게 동작하기 때문에 이 함수를 비트 연산자로 구현할 수 있다면 더 빠른 결과를 기대할 수도 있다.

같은 기능을 비트 연산자를 사용해서 구현해보자. 원 문제의 의도에 맞게 비트 연산자를 써서 실제 각 자릿수의 비트에 접근해 0/1 여부를 확인해서 더하도록 하자. 어떻게 하면 될까? 1장 1절의 내용을 응용하면 될 것 같다.

코드는 다음과 같다.

def bit_count(n):
    k = 0
    count = 0

    while n >= (1 << k):
        if n & (1 << k) != 0:
            count += 1
        k += 1

    return count

print('1000은 2진수로', bin(1000), '이고, 1의 개수는', bit_count(1000), '개입니다.')

1000은 2진수로 0b1111101000 이고, 1의 개수는 6 개입니다.

새로 정의한 bit_count 함수는 자릿수를 뜻하는 k 변수를 0으로 설정해놓고 시작한다. 그리고 탐색할 n 에 대해서 0번째, 1번째, …번째 자릿수에 대해 비트가 켜져 있는지 확인한다. 논리식은 1장 1절에서 쓴 식을 그대로 가져다 썼다. 그리고 만약 k번째 비트가 켜져 있다면, & 연산 결과가 0이 아니라면 count 를 1 키운다. k 는 반복문 블락이 한 번 실행된 뒤에 1 키운다.

이 식은 앞선 함수보다 더 길다. 하지만 비트를 사용한다는 느낌이 강하게 든다. 확실히 0번째 비트부터 포함해 각 자릿수를 모두 훑고 있다. 이 함수도 비트 연산자를 쓰면서 한 줄로 만들 수 있을까? 한 번 시도해보길 바란다.

3.3. Boolean값 Toggle하기

앞선 두 개의 트릭이 실제 개발보다는 알고리즘 문제와 보다 관련이 있었다면 이 트릭은 실제 개발에서 쓸모가 있다. 바로 Boolean값 Toggle(이하 “토글”)하기이다. 쉽게 말해 비트가 On 상태면(1이면) Off로 꺼버리고, Off 상태면(0이면) On 상태로 바꾸는 작업이다. 이런 작업은 일상에서 쉽게 찾아볼 수 있다. 전등 켜고 끄는 것도 토글이고, 노트북 전원 켜고 끄는 것도 토글이다.

이 작업은 개발에서도 쉬이 접할 수 있다. 이는 최근 개발 과제에서 실제로 했던 작업인데 자바스크립트로 특정 버튼을 누르면 연결된 HTML 엘레멘트의 전원을 켜고 끄는 토글을 구현했다. 페이스북의 특정 포스트를 ‘좋아요’를 켜고 다시 눌러 끄는 작업 등이 말 그대로 토글이다.

먼저 비트 연산자를 쓰지 않고 이 작업을 해보자. 어떤 기능에 쓰이는 bool 변수 onoff를 토글하는 코드는 기본적인 조건문으로 만들 수 있을 것이다.

onoff = True

if onoff == True:
    onoff = False
else:
    onoff = True

가장 정직하고 무식한 코드다. 4줄이나 차지하는 조건문은 삼항연산자로 개선할 수 있다.

onoff = False if onoff else True

일단 한 줄로는 만들었다. 이렇게도 실제 기능구현에서 충분히 쓸 수 있겠지만 정말 바람직한지는 모르겠다.

이 작업을 비트 연산자로 구현하면 다음과 같다.

onoff ^= True

XOR 연산자 ^를 써서 한 줄로 만들었다. 이 코드는 onoff 가 True이면 True와 만나 False을 반환하고, onoff 가 False이면 True를 반환하게 한다. 바로 위의 삼항연산자 코드보다 더 가볍고 눈에 확 들어온다. 무엇보다 비트 연산자는 고급언어 사이에서 통용되지만 파이썬 삼항연산자는 C나 자바 등 다른 고급언어의 삼항연산자와 문법이 다르기 때문에, 파이썬을 완벽하게 읽지 못하는 사람에게도 가독성을 보장하는 바람직한 효과가 있다.

간단하게 테스트해보자.

onoff = True
onoff ^= True
print(onoff)

onoff = False
onoff ^= True
print(onoff)


False
True

더 이상의 설명이 필요한가? 앞으로 토글이 필요할 땐 꼭 이 방식이다! 약속했다?

4. 집합론과 비트의 만남

이번 포스트의 핵심내용이라고 말할 수 있다. 학문과 학문의 만남은 언제나 설레고 즐겁다. 종만북의 비트 연산 챕터를 읽으면서 비트 연산이 집합론과 접점을 가지고 있음을 깨닫고 크게 통찰한 기억이 있다. 생각해보면 비트 연산 관련 포스트를 작성하기로 한 이유 중 큰 부분은 이 내용을 정리하고 싶어서였는지도 모르겠다.

포스트를 준비하면서 ‘집합론과 비트가 접점이 있을 수밖에 없구나’하고 느꼈다. 생각해보면 특정 원소가 어떤 집합에 속하는지는 Yes or no, 즉 boolean 값으로 표현할 수 있다. 비트가 0과 1의 값만 가질 수 있는 것과 이렇게 유사하구나. 이들의 접점은 다른 좋은 예제들에서 많이 살펴볼 수 있겠지만 일단은 내가 공부하고 크게 감명받은 한 가지 연산을 통해서 알아보도록 하자. 이를 위해서 먼저 어떤 2진수를 집합으로 표현해보고, 그 표현을 바탕으로 비트 집합의 차집합 예제를 통해 둘의 접점을 확인하자.

4.1. 2진수의 집합 표현

이들의 접점을 확인하기 위해서는 먼저 양의 정수 2진수 n을 집합으로 표기할 수 있어야 한다. 처음에는 뜬구름 잡는 소리같다. 어떻게 2진수를 집합으로 표현할 수 있을까? 2진수는 1개 이상의 1과 0으로 이루어지는데, 집합은 같은 원소의 중복을 허용하지 않으니 말이다. 핵심은 특정 비트값 1 또는 0에 집중하는 것이 아니라 2진수 n에서 1로 켜져 있는 k번째 자릿값을 집합의 원소로 하는 것이다. 이를 구현하는 함수를 정의해보자.

\[ \displaylines{ \text{임의의 양의 정수 } n \text{에 대해서,} \\ func(n) = n \text{을 이진수화했을 때 비트가 1로 켜져 있는 자릿수를 원소로 하는 집합을 반환하는 함수} } \]

아직 이해가 확실하지 않다면 예를 통해서 한 번 더 확인하자.

\[ \displaylines{ 210 = 1101 \text{ } 0010_{(2)} \\ \textbf{func(210) = {1, 4, 6, 7}} } \]

10진수 210은 2진수로는 \(1101 \text{ } 0010_{(2)}\)이다. 총 8개의 비트로 이루어진 수인데 이때 1, 4, 6, 7번째 비트가 1로 켜져 있다. func 함수는 양의 정수를 2진수로 변환했을 때 비트가 1인 자릿수의 번호를 원소로 하는 집합을 반환하는데 반환된 값은 위와 같다. 이때 최소한 양의 정수 n에 대해서 10진수 표현과 그에 대한 func 집합 표현은 서로 일대일 대응한다. 다시 말해, 임의의 한 10진수에서 func 집합을 유일하게 하나만 만들 수 있고, 반대로 임의의 func 집합에서도 10진수를 유일하게 하나만 만들 수 있다.

양의 정수 n을 1로 켜져 있는 비트 자릿수의 집합으로 표기할 수 있다는 이해를 바탕으로 다음 절로 넘어가자.

4.2. 차집합: 비트 연산으로 구현하기

차집합(difference of sets)은 기본적인 집합 연산 중 한 집합에서 다른 집합의 원소를 빼는 연산을 의미한다.

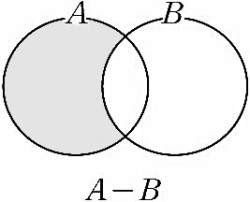
Simple example of difference of sets

위 사진은 차집합의 간단한 예 중 하나로 집합 A에서 집합 B를 뺀 예제를 보여주고 있다.

이제 본격적인 예로 넘어가자. 우리가 하고 싶은 것은 \(func(n)\)에 대해 차집합을 하고 싶은 것이다. \(func(210) = \{1, 4, 6, 7\}\)과 같다. 이때 \(func(210) - \{4\}\)은 차집합 연산으로, \(func(210)\) 집합에서 4 원소만을 갖는 부분집합을 빼겠다는 것과 동일하다. \(\{1, 4, 6, 7\} - \{4\} = \{1, 6, 7\}\)이기 때문에 이 집합을 10진수로 다시 옮기면 \(\{1, 6, 7\}\), 즉 194(210 - \(2^4\))이 될 것이다. 차집합의 개념과 일치한다.

\[ func(210) - \text{{4}} = \text{{1, 6, 7}} \]

\(A - B\)를 어떻게 비트 연산으로 구현할까? -를 사용한 표현은 간단하지만 어떻게 구현할지 정확히 발상이 떠오르지 않는다. 대신 \(A - B\)의 다른 표현을 사용하도록 하자.

\[ A - B = A \cap B^\complement \]

A 차집합 B는 우측식과 정확히 일치한다. 내 기억에 고등학교에서 배우는 내용인데 이 정도는 외우고 있어도 나쁘지 않다. 우측에서 쓰인 집합 연산자들은 모두 비트 연산자와 대응되기 때문에 이를 그대로 이용할 것이다.

\(func\) 함수를 정의한 것처럼 다른 함수 \(diff\)를 정의하자. 이 함수는 양의 정수 \(n\)과 \(d\)를 받아 \(func(n)\)에서 \(d\) 번째 비트 집합을 뺀 차집합을 10진수 형태로 반환한다.

\[ diff(n, d) = func(n) - {d} = func(n) \cap {d}^\complement \]

이를 그대로 함수로 옮기면 다음과 같다.

def diff(n, d):
    return n & ~(1 << d)

비트 연산이 익숙하지 않다면 헷갈릴만한 식이다. 하지만 3가지 핵심 포인트만 살피면 된다.

&는 비트 AND 연산자으로 교집합을 의미하는 \(\cap\) 집합 연산자와 대응된다.
(1 << d)는 앞서 살펴봤듯 d 번째 비트를 켠다를 의미한다.
- 함수의 의도는 d 번째 비트를 원소로 하는 집합을 빼는 것이기 때문에 이를 사용한다.
~는 비트 여집합 연산자로 \(^{\complement}\) 여집합 연산자와 대응된다.
- 이 대응은 컴퓨터 과학과 관련이 있는데 수를 표현하는 메모리 공간에서 ~를 쓰면 0이었던 비트가 모두 1로 켜지고 1이었던 비트들은 꺼진다. 그래서 정확히 집합의 여집합 연산자와 대응된다.

먼저 잘 작동하는지 확인하자.

print(15, '는 ', bin(15), '이고 여기서 ', 2, '번째 비트 집합을 빼면 ', bin(diff(15, 2)), '이 됩니다.', sep='')
print(32, '는 ', bin(32), '이고 여기서 ', 5, '번째 비트 집합을 빼면 ', bin(diff(32, 5)), '이 됩니다.', sep='')
print(100, '는 ', bin(100), '이고 여기서 ', 5, '번째 비트 집합을 빼면 ', bin(diff(100, 5)), '이 됩니다.', sep='')
print(210, '는 ', bin(210), '이고 여기서 ', 4, '번째 비트 집합을 빼면 ', bin(diff(210, 4)), '이 됩니다.', sep='')


15는 0b1111이고 여기서 2번째 비트 집합을 빼면 0b1011이 됩니다.
32는 0b100000이고 여기서 5번째 비트 집합을 빼면 0b0이 됩니다.
100는 0b1100100이고 여기서 5번째 비트 집합을 빼면 0b1000100이 됩니다.
210는 0b11010010이고 여기서 4번째 비트 집합을 빼면 0b11000010이 됩니다.

모두 잘 동작한다. 이해를 위해 빼는 집합을 하나의 원소만 가지고 있는 예제만 사용했는데 여러 개의 원소를 갖는 비트 집합도 얼마든지 구현 가능하다.

4.3. 그게 최선입니까? 확실해요?

2절에서 비트 차집합 연산이 잘 동작하는 것은 확인했다. 근데 많은 독자들은 ‘왜 비트 차집합을 구현하는 데 저렇게까지 복잡한 비트 연산자를 사용하지?’라는 질문을 충분히 할 수 있다.

\[ diff(n, d) = func(n) - {d} = func(n) \cap {d}^\complement \]

diff 함수는 우측의 식을 그대로 비트 연산자로 옮겼다. 하지만 ‘중앙식을 그대로 함수로 옮겨도 충분하지 않나?’라는 생각도 충분히 할 수 있다. diff 를 수정해 이를 반영해보자.

def diff(n, d):
    return n - (1 << d)

확실히 이 식이 이해하기에는 훨씬 쉽다. 그럼 이를 그대로 사용하면 될까?

Simple example of difference of sets

정답은 ‘아니다’이다. 그 이유는 집합에서의 ‘뺄셈’, 즉 차집합과 수에서의 ‘뺄셈’이 개념상 차이가 있기 때문이다. 그림에서 보면 ‘A에서 B를 빼는 것’은 ‘A에서 A와 B의 교집합(\(A \cap B\))을 뺀다는 것’과 동일한 의미이기 때문에 교집합이 공집합(\(\emptyset\), empty set)이라면 A에는 연산 전과 후의 차이가 없다.

2절에서 diff 함수가 잘 동작하는지 확인한 코드에서 빼는 대상이 되는 비트는 의도적으로 n 에서 이미 1로 켜져 있던 상태였다. 다시 말해 피연산자들의 교집합이 공집합이 아니었다. 그런데 만약 교집합이 공집합이라면? 집합론의 개념대로라면 원 수 n 은 차집합 연산 후에도 값이 변하지 않아야 한다. 하지만 새로 만든 diff 는 교집합이 공집합일 때 n 의 값을 변화시킨다.

def diff(n, d):
    return n - (1 << d)

print(32, '는 ', bin(32), '이고 여기서 ', 3, '번째 비트 집합을 빼면 ', diff(32, 3), '이 됩니다.', sep='')
print(100, '는 ', bin(100), '이고 여기서 ', 5, '번째 비트 집합을 빼면 ', diff(100, 5), '이 됩니다.', sep='')
print(210, '는 ', bin(210), '이고 여기서 ', 4, '번째 비트 집합을 빼면 ', diff(210, 4), '이 됩니다.', sep='')


32는 0b100000이고 여기서 3번째 비트 집합을 빼면 24이 됩니다.
100는 0b1100100이고 여기서 5번째 비트 집합을 빼면 68이 됩니다.
210는 0b11010010이고 여기서 4번째 비트 집합을 빼면 194이 됩니다.

새로 만든 함수에 테스트 코드를 적용했다. 코드를 조금 수정해서 원 수의 비트가 0인 비트로 d 인자를 바꾸고, 연산 전과 후의 값을 비교하기 위해 결과를 2진수가 아닌 10진수로 출력했다. 그러자 확실히 연산 전후의 결과가 다르다. 위와 같이 집합 빼기와 숫자 빼기는 엄연히 다르기 때문에 단순히 뺄셈을 적용하지 말고 첫 번째 식과 같이 적용해야 한다.

5. 마치며

포스트가 꽤 길어졌다. ‘설명이 너무 길어서 그런가’하는 생각이 드는 것도 사실인데 그래도 내 타겟 독자층은 초심자 분들이기 때문에 일단 이대로 가보려한다.

이 포스트는 말했듯이 재미있거나 유용한 비트 연산을 더 찾으면 내용을 추가할 생각이다. 재미있거나 유용한 연산을 알고 있는 분들은 제보해주시면 감사히 적용할 수 있도록 하겠다.

내 포스트 중 비스마스킹을 적용한 예제로 에라토스테네스의 체를 비트마스킹으로 구현한 포스트가 있다. 비트마스킹을 좀더 다뤄보고 싶은 분들은 이 예제도 확인하면 괜찮겠다.

이상 포스트를 마칩니다. 감사합니다. :)

6. 자료 출처

『알고리즘 문제 해결 전략』16장 비트마스크, 구종만, 인사이트(insight)