에라토스테네스의 체 Bitmask로 구현하기
0. 들어가며
에라토스테네스의 체는 정해진 범위 내의 자연수에서 소수를 걸러내는 데 유용하게 사용되는 알고리즘이다. 이를 개발한 에라토스테네스는 기원전 200여년 전 사람인데 참 대단하다는 생각이 든다. 소수론은 워낙 중요한 분야라 소수를 판별하는 것과 관련된 수많은 알고리즘이 있지만, 수학자가 아닌 평범한 개발자 정도라면 에라토스테네스의 체(이하 “체”) 알고리즘 정도는 1부터 \(\sqrt{n}\)까지 나눠보는 간단한 소수 판별법과 함께 모두 알 것이라 생각한다. 나도 체는 한참 전에 만들어본 기억이 있다.
최근 어렴풋이 알고 있던 비트 알고리즘을 좀더 깊이 공부했는데 공부하는 책에서 비트마스킹을 활용해 체의 공간 효율을 상당 부분 개선할 수 있는 방법을 알고 충격을 받았다.
그래서 이번 포스트에서는
- 비트마스크를 활용한 체를 구현하고
- 비트 연산자가 활용된 코드는 비교적 가독성이 떨어지기 때문에 사용자 인터페이스를 고려해 제품화해보자.
이 포스트의 핵심 알고리즘은 “종만북”의 16장 ‘비트마스크’장에 크게 빚지고 있다. 제정신 아닌 코드를 소개해준 것에 진심으로 감사드린다.
에라토스테네스의 체와 기본적인 비트마스크 정도의 개념은 이해하고 있을 것이라 가정하고 진행한다.
1. 기본적인 구현
먼저 비트마스크는 사용하지 않은 일반적인 체를 구현해보자. 당연히 파이썬을 사용하며 원하는 SIZE에 맞게 체를 선언하고 2부터 SIZE까지 소수 판별 작업을 한다.
SIZE = 2 ** 16
SIZE_SQRT = int(SIZE ** (1/2))
sieve = [1 for _ in range(SIZE+1)]
sieve[0] = sieve[1] = 0
TEST = 20
for i in range(2, SIZE_SQRT+1):
if sieve[i] == 1:
for j in range(i*i, SIZE+1, i):
sieve[j] = 0
for i in range(2, TEST+1):
print(f"{i:>3} : {'prime' if sieve[i] else 'composite'}")
평범한 코드다. 체의 크기는 2의 16승으로 잡고(이는 임의의 값을 줬다) 1로 초기화한다. 2부터 for 문을 돌며 값이 1로 되어 있으면 그 수의 배수는 모두 0으로 처리한다. 전혀 어려울 것이 없는데 배수를 처리하는 j 의 시작값을 i*i 로 한 것만 유의하면 된다. 가령 3의 배수를 지울 때, 6 같은 경우는 2의 배수로 이미 지워져 있을 것이기 때문에 다시 지울 필요가 없고, 3의 제곱인 9부터 지워나가면 된다.
참고로 2부터 20까지 테스트하는 테스트 코드에서 ‘composite’는 ‘합성수’라는 뜻이다. 모든 자연수는 1과 소수, 합성수로 이루어지는데 합성수는 약수가 3개 이상인 수라고 생각하면 될 듯하다. 이번에 공부하면서 ‘composite’라는 단어를 처음 배워서 짚고 넘어간다.
2. 핵심 아이디어
2.1. 에라토스테네스의 체의 장단점
다른 소수 판별 알고리즘과 비교해서, 체 알고리즘의 장단점은 뭐가 있을까?
일단 장점은 구현하는 방법이 매우 쉽다는 것이다. 소수를 판별하는 수많은 연구가 있었고, 효율적인 알고리즘이 많지만 상당수는 나같은 일반인이 이해하기 너무 어려운 것들이 많다. 하지만 체는 최소한의 수학 지식만 있으면 쉽게 구현할 수 있다. 또 다른 장점은 일정 범위 내의 소수를 모두 계산할 수 있다는 것이다. 이는 일정 범위 내의 자연수에서 소수 판별을 빈번하게 해야 한다면 상당한 캐시 효율을 낼 수 있다는 의미이기도 하다.
하지만 결정적인 단점으로 간단히 몇 개의 계산만 하려고 해도 1부터 원하는 수까지의 모든 수를 계산해야 하고, 그래서 만약 판별하려는 수가 크다면 공간을 많이 잡아 먹는다. 가령 1부터 2의 32승까지 체를 계산한다고 할 때, 기본적인 구현은 비트맵으로 자연수 n 이 소수인지 아닌지를 체의 n 인덱스에 1, 0으로 저장한다. 때문에 체를 4바이트 정수 배열로 구현해도 약 4GB의 메모리가 필요하다고 한다. 이 단점으로 인해 우리는 체의 공간 비효율을 어떻게 더 개선할 수 있을까 하는 질문을 던졌고, 그 후보로 체를 비트마스크를 동원해 구현하는 방법이 제안되었다.
2.2. 공간 비효율을 개선하자: 비트마스크를 통해
앞선 절에서 체의 단점은 판별하려는 수가 클 때 공간이 많이 낭비되는 것이라고 살펴봤다. 앞선 기본적인 구현은 비트맵으로, 배열의 원소 하나가 해당 원소의 인덱스의 소수 여부를 1과 0으로 담고 있다. 이를 어떻게 개선할 수 있을까?
공간이 문제라면, 원소 하나에 숫자 하나의 소수 여부만 담는 작금의 방식을 개선하면 되지 않을까? 그러니까, 배열의 원소 하나에 여러 숫자의 소수 여부를 담으면 확실히 배열의 크기를 줄일 수 있을 것 같다.
내가 만드려는 체의 크기를 SIZE 라고 하자. 그리고 한 원소는 4바이트 정수를 쓴다고 하자.
그리고 내가 판별하려는 소수가 7이기 때문에 체의 크기가 7이라고 하자. 배열의 크기는 8 * 4, 즉 32 바이트가 될 것이다. 왜 7이 아닌 8를 곱했냐고 하면 당연하다. 크기를 7로 잡으면 배열의 마지막 인덱스가 6이니까 7을 판별할 수 없다. 다 아시겠지만 무시하는 것이 아니고 그냥 적었다. ㅋㅋ
이때, 우리가 하려는 공간 절약은 비트마스크를 통해 실현된다. 기본적인 구현에서 한 원소는 0과 1의 값만 갖는데 이는 한 원소에 1개의 비트만 할당된다고 말할 수 있다. 1개의 비트를 통해 하나의 수의 소수 여부를 담을 수 있다.
그렇다면 만약 한 원소에 8개의 비트를 담는다면 그 비트들을 통해 8개의 수의 소수 여부를 담을 수 있지 않을까?
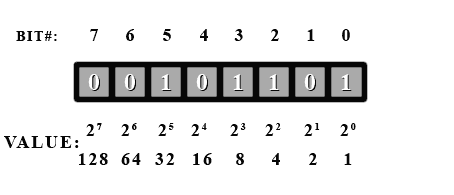
위 그림은 어떤 8비트 이진수다. 이 수를 표현하기 위해 8개의 비트가 사용되었다. 각 비트는 0부터 7까지의 인덱스를 갖는데, 아까 예에서 한 원소에 1비트만 담는 대신, 한 원소에 8비트 수를 담으면 각 비트의 0, 1 상태를 통해 0부터 7까지 8개의 자연수의 소수 여부를 알 수 있다. SIZE 가 7일 때, 체의 단 하나뿐인 원소에는 다음과 같은 값이 실릴 것이다.
[10101100_{2}]
이 8비트 이진수는 오른쪽에서부터 0부터 7까지의 소수 판별 여부를 담고 있으며 2, 3, 5, 7은 소수이기 때문에 비트가 켜져 있는 것을 알 수 있다.
배열의 한 원소에 비트를 한 개만 쓰는 일반적인 구현 대신, 한 원소에 비트를 8개씩 쓰는 비트마스크 기법을 통해, 필요한 배열의 크기는 SIZE / 8 로 절약될 수 있다. SIZE 가 7일 때, 배열의 크기가 1이 된 것을 통해 알 수 있다.
이를 알고리즘으로 구현하자.
3. 구현
이 알고리즘의 핵심 아이디어는 기본적인 구현이 체의 한 원소에 0과 1, 즉 1비트만 담음으로써 단 한 개의 자연수의 소수 여부만 담을 수 있던 것과 달리 비트마스크 구현은 한 원소에 8비트씩을 담음으로써 8개의 자연수의 소수 여부를 파악할 수 있고 따라서 필요한 배열(체)의 크기를 8분의 1로 줄일 수 있다는 것이다.
그건 그렇다치고, 이제 이것을 어떻게 실현하는가가 문제이다. 해결해야 하는 주된 문제는 이것이다.
체가 판별하려는 최대 숫자가 SIZE 이고 내가 현재 판별하고자 하는 숫자가 n일 때
- 현재 체의 크기는 SIZE / 8 일텐데, 내가 원하는 n 은 체의 몇 번째 원소에 들어 있는가?
- 해당하는 원소를 찾았을 때 원소 안의 8비트 수의 어느 비트가 내가 원하는 n 의 소수 여부를 담고 있는가?
이 두 문제를 해결하면 동시에 해결하면(AND) 우리가 원하는 수의 소수 여부를 찾을 수 있다.
먼저 1번. 원하는 수는 체의 어느 원소에 들어있을지. 일반적인 구현에서는 단순히 sieve[n] 을 통해 그 여부를 알 수 있었는데 지금은 단순히 n 을 넣어서는 안 된다. 여기서는 sieve[n >> 3] 를 통해 원소 위치를 찾을 수 있다. 사실 ‘n >> 3’은 기능상 ‘n // 8’과 일치한다.
2번. 체의 원소를 찾았을 때 8비트에서 내가 원하는 원소는 어느 비트에 위치할지. 이는 ‘1 << (7 & n)’으로 찾을 수 있다. ‘7 & n’을 통해 n 의 7과의 접점을 찾는다. 그러니까 둘의 ‘&’ 연산은 0부터 7까지의 값을 내놓을 것이고, 이는 사실상 ‘n % 8’과 같다. 그 나머지를 ‘(1 << ‘ 연산으로 원소의 8비트 이진수에서 원하는 비트에 접근할 수 있다.
이 1번과 2번의 교집합을 찾으면 수많은 수에서 우리가 원하는 바로 그 수의 소수 여부를 판단할 수 있다. 코드를 살펴보자.
# 1.
SIZE = 2 ** 16 + 1 # Size is too big... Isn't it?
# 2.
sieve = [255 for _ in range(SIZE // 8 + 1)]
# 3.
def set_composite(n):
sieve[n >> 3] &= ~(1 << (n & 7))
# 4.
set_composite(0)
set_composite(1)
# 5.
def is_prime(n):
return True if sieve[n >> 3] & (1 << (n & 7)) else False
# 6.
for i in range(2, int(SIZE ** (1/2))+1):
if is_prime(i):
for j in range(i*i, SIZE+1, i):
set_composite(j)
각 부분을 살펴보자.
- 먼저 체의 크기 SIZE 는 2의 16승이다. 대단한 의미는 없다.
- 체의 크기를 ‘SIZE // 8’ 로 잡는다. 그리고 각 원소를 255로 초기화한다. 255는 8개의 비트를 모두 1로 켠 수이며 기본적인 구현에서 각 원소를 1로 초기화한 것과 일맥상통하다.
- 원하는 수 n 합성수로 설정하는 set_composite 함수를 만들었다. 이 함수는 먼저 n 이 속한 체의 원소를 찾고(‘sieve[n >> 3]’), 그 수에서 n 이 속한 비트를 0으로 설정한다.(‘&= ~(1 << (n & 7)’). 이 코드는 몇 가지 예를 만들어 실험해보라.
- 그리고 0과 1은 소수가 아니기 때문에 합성수로 설정한다. 엄밀히 말해 0, 1 모두 합성수는 아니지만 이 예제에서는 소수가 아닌 것만 확인하면 된다.
- n 이 소수인지 판단하는 is_prime 함수를 만든다. 이는 앞서 살펴 본 1번과 2번의 교집합(‘&’)을 살핀다. 교집합 비트가 0이면 소수가 아니고, 0이 아니면 소수다.
- 2부터 각 수에 대해 체 작업을 한다. 이는 기본적인 구현의 알고리즘과 본질적으로 같다.
한 번 테스트해보라.
4. 제품화
4.1. 제품화의 필요성
난 위의 비트마스크 체 코드를 제품화할 필요가 있다고 강력하게 느끼고 있다. 그 이유는 크게 두 가지가 있다.
먼저 비트마스크는 인간에게 직관적이지 않은 2진수 비트를 다루기 때문에 위 코드를 실제 체의 사용자들에게 공개하는 것은 바람직하지 않다.
또한 체를 구현할 때는 어떤 수 n 이 소수인지를 일회성으로 판단하는 경우보다는, 체를 만들어놓고 일정 범위 안에서 빈번히 재활용하려는 경우가 많다. 많이 사용하는 프로그램은 사용하기 편해야 한다.
이런 이유로 난 위의 체 코드를 클래스를 통해 구현하는 것이 적절하다고 생각했다. 구체적인 코드는 감추고 추상화된 체에 필수적인 인터페이스만 제공하면 사용자는 어려운 비트마스크 따위는 걱정할 필요 없이 행복하게 체를 쓸 수 있을테니까.
내가 제안하는 코드는 다음과 같다.
4.2. 클래스로 구현한 비트마스트 체
SIZE = 2 ** 16 + 1 # Size is too big... Isn't it?
class Sieve:
def __init__(self, size):
self._size = size
self._sieve = [255 for _ in range(SIZE >> 3 + 1)]
self._set_composite(0)
self._set_composite(1)
for i in range(2, int(self._size ** (1/2))+1):
if self.is_prime(i):
for j in range(i*i, self._size+1, i):
self._set_composite(j)
print(f"Sieve of size {size} is initialized")
def is_prime(self, n):
if n > self._size:
raise ValueError(f"This sieve only support integers equal to or less than {self._size}")
return True if self._sieve[n >> 3] & (1 << (n & 7)) else False
def _set_composite(self, n):
self._sieve[n >> 3] &= ~(1 << (n & 7))
sieve = Sieve(SIZE)
위 코드의 핵심 알고리즘은 앞선 코드와 똑같다. 다만 구체적인 코드를 캡슐화해 핵심적인 API만 남겼는데 체에서는 ‘is_prime’ 이 된다.(체를 만드는 이유가 그거니까.)
눈여겨 볼 점은 필수적인 API를 제외한 Sieve 클래스의 ‘size’, ‘sieve’, ‘set_composite’ 특성 앞에 ‘_‘를 붙임으로써 이 특성들은 보호 속성이며 사용자가 건드리지 않는 것이 바람직하다고 암시하고 있다는 것이다. 확실히 체나 합성수를 설정하는 함수를 사용자가 만져서 좋을 것은 별로 없어보인다. 이를 ‘_‘를 두 개 쓰는 ‘private’이 아닌 ‘protected’ 속성으로 한 것은 이유가 있다. 향후 확장성의 여지가 있다고 생각했기 때문이다. 지금은 인스턴스를 생성할 때 설정한 체의 크기를 수정할 수 없다. 하지만 이 클래스를 상속해 체의 크기를 늘리는 등의 재밌는 활동이 가능하다고 생각했다. 그 여지를 남겨두기 위해 사용자의 개입 여지를 남겼다.
4.3. Customization을 조금만 더…
저 정도 코드도 사실 훌륭하다. 근데 사실 저 알고리즘을 책에서 처음 접했을 때 느낀 생각은 ‘일반적인 정수 배열을 쓰면 한 원소에 4바이트가 할당될테고 그러면 32비트 숫자까지 담을 수 있는데 왜 8비트까지만 담지?’였다. 8비트가 아니라 16비트를 담으면 체의 크기를 16분의 1로 줄일 수 있을텐데? 반대로 한 원소에 4비트만 담고 싶을 수도 있잖아? 사용자의 필요과 수요는 우리의 상상을 언제나 초월하기 마련이다.
이왕 많은 사용자를 고려한 제품화를 시작한 이상 체의 원소에 담기는 비트의 수를 조절할 수 있는 인자를 추가하자. 조절되는 비트 수는 2, 4, 8, 16처럼 2의 제곱수들을 대상으로 하기 때문에 이 숫자들의 지수(1, 2, 3, 4)를 받으면 될 듯하다. 최종적으로 완성된 비트마스크 체는 다음과 같다.
SIZE = 2 ** 16 + 1 # Size is too big... Isn't it?
class Sieve:
"""Sieve of Eratosthenes in bitmask version
It supports bitmasking for implementing the sieve internally
so you can save space.
"""
def __init__(self, size, expo=3):
"""Initialize the sieve with given size and expo
:input:
size: INT | Total size of the sieve. You cannot change it. Think carefully.
expo: INT | The number of exponentials to use bitmask. Default value is 3.
That means one element in the sieve contains 8 bit(2 ^ 3) integers.
:return:
None. You can now use the sieve with 'is_prime' method.
"""
self._size = size
self._expo=expo
self._sieve = [(1 << (1 << self._expo) - 1) for _ in range((SIZE >> self._expo) + 1)]
self._set_composite(0)
self._set_composite(1)
for i in range(2, int(self._size ** (1/2))+1):
if self.is_prime(i):
for j in range(i*i, self._size+1, i):
self._set_composite(j)
print(f"Sieve of size {size} is initialized")
def is_prime(self, n):
"""Check if the given n is prime or not
If n is over than the size of the sieve, raise value error.
"""
if n > self._size:
raise ValueError(f"This sieve only support integers equal to or less than {self._size}")
return True if self._sieve[n >> self._expo] & (1 << (n & ((1 << self._expo)-1))) else False
def _set_composite(self, n):
"""Set the given n composite number in the sieve"""
self._sieve[n >> self._expo] &= ~(1 << (n & ((1 << self._expo)-1)))
sieve = Sieve(SIZE)
좀더 개선된 이 체 클래스는 초기화 시 한 원소에 담길 비트 수의 2의 지수를 지정하는 expo 변수를 받는다. 체의 한 원소에 2의 expo 승만큼의 비트가 담길 예정이며 기본값은 3으로 했다. 특별한 의미는 없고 처음 만들었을 때 8개 비트를 저장해서 그렇게 했다.
그 변수를 이용해 코드의 매직넘버들을 모두 갈아야 한다. 가령 처음 만든 체 클래스에서 사용된 7, 255, 3 등은 모두 2의 3승인 8과 관련이 있는 매직넘버들이었다. 이때는 체의 한 원소에 담길 비트를 무조건 8비트로 지정했지만 이제는 사용자가 지정할 수 있으므로(Customization!) 모두 그에 맞게 바꾼다.
위와 같이 바꿔서 코드는 사실 더 어려워졌다. 하지만 그게 중요한가? 대부분의 사용자는 실제 코드에 접근하지 않을 것이고 대신 사용자는 자신의 의도에 맞게 체의 크기를 줄이고 늘일 수 있다. 이 얼마나 행복한가?
마지막으로 훌륭한 프로그램의 기본인 문서화도 잊지 않는다.
5. 마치며
이번 포스트에서는 일반적인 에라토스테네스의 체 알고리즘에서 비트마스크를 통해 공간 효율을 개선했다. 그 알고리즘도 알고리즘이지만 클래스를 통해 추상화하고 인터페이스만 남겼다는 개념이 이 포스트의 의의인 것 같다. 우리는 언제나 사용자를 고려해야 한다. 종만북의 알고리즘을 그대로 복붙하지 않고, 이를 활용해 내 포스트를 만들었다는 자부심이 개인적으로 생긴다. 이렇게 지식은 발전한다.
이상 포스트를 마칩니다.
