
TSP 알고리즘 2: 동적 계획법 구현
0. Index
- 들어가며
- 구현을 위한 통찰
- 2.1. 완전탐색 코드 재확인
- 2.2. 중복 확인
- 2.3. 시작 도시도 중요하지 않다
- 실제 코드
- 마치며
1. 들어가며
이전 포스트에서 TSP에 대한 문제 소개와 완전탐색 구현코드를 살펴봤다. 이번 포스트에서는 완전탐색 코드를 바탕으로 TSP를 동적 계획법으로 구현해본다. 이때 최대한 시간복잡도를 낮추기 위한 세 가지의 통찰을 살피고 코드를 구현한다.
2. 구현을 위한 통찰
2.1. 완전탐색 코드 재확인
우리의 종만 형님께서는 완전탐색은 많은 경우 동적 계획법으로 개선가능하다고 말씀하셨다. 이를 확인하기 위해 이전 포스트에서 기술했던 find_path 함수를 다시 살펴보자.
find_path(start, last, V, tmp_dist):
- 여행을 start에서 시작했고,
- 현재까지 방문한 중간 경로의 마지막 도시는 last이고,
- 방문한 도시의 집합은 V,
- 중간경로의 길이는 tmp_dist일 때
해당 중간경로를 사용해서 여행을 마쳤을 때의 완성된 모든 경로의 길의의 최소값을 구하라.
실제 값을 구하는 함수를 문장으로 기술했다. 이 함수는 4개의 인자를 받는다.
- 시작 도시
- 중간 경로의 마지막 방문 도시
- 방문한 도시의 집합
- 중간 경로의 길이
완전탐색에서는 이 인자를 모두 사용했지만 동적 계획법에서는 가능한 인자를 줄이고, 실제로 같은 인자에 대한 호출이 여러 번 일어나는지 확인해야 한다. 실제 동적 계획법 코드를 살피기 전에 몇 가지 통찰을 살펴본다.
2.1. 구체적인 경로는 중요하지 않다.
문장으로 기술된 함수에서 세 번째 인자는 방문한 도시의 집합이다. 이때 재미있는 것은 방문한 중간 경로의 구체적인 순서는 중요하지 않다는 것이다. 실제 완전탐색 코드에서 방문한 도시의 집합을 비트 연산을 통해 구현했다.
실제 경로(V)를 list 자료구조를 써서 표현할 수도 있었지만 그렇게 하지 않은 것은 비트를 쓰는 것이 조금 더 빠르기도 해서인 것도 있다. 하지만 가장 중요한 이유는 비트로 방문한 도시 집합을 표현하면 실제 구체적인 경로는 표현되지 않는데, 그럼에도 정답이 잘 나온다는 것을 보여주기 위한 것도 있다. 코드에서 확인할 수 있듯이 중요한 것은 여행 시작 도시와 현재 중간 경로에서의 마지막 방문 도시, 그리고 각 도시의 방문 여부이다. 구체적인 경로, 도시의 방문 순서는 중요하지 않다. 이것이 첫 번째 통찰이다.
2.2. 중복 확인
다음으로는 특정 start, last, V에서 이들을 활용한 find_path(start, last, V) 가 실제 중복 호출되는지 확인해야 한다. 이것이 확인되어야 동적 계획법이 실효성을 갖는다.
아, 마지막 인자 tmp_dist 는 어디 갔냐고 물을 수 있다. 확인결과 이 tmp_dist 인자는 함수 호출에 직접 넣지 않고도 값을 구할 수 있다는 것을 알 수 있게 되었다. 이는 실제 코드를 보고 이야기하자.
특정 start, last, V에 find_path 에는 다음과 같은 수식이 성립한다.
\[ find\_path(start, last, V) = MIN \bigg( \forall c \in V^\complement | find\_path(start, c, V \cup {c}) + D[last][c] \bigg) \]
이 수식은 다음과 같은 의미를 가진다:
특정 start, last, V 에 대해 아직 방문하지 않은 모든 도시 각각을 방문하는 재귀함수를 호출하고 이중 최소값을 취한다.
조금만 생각해보면 당연한 것이다. 그러면 이제 특정 start, last, V에 대한 find_path 가 두 번 이상 호출되는지 확인해보자. 대단한 수식 증명까지 갈 것도 없이(사실 어떻게 하는지 잘 모르겠다) 간단한 예를 들어보면 되겠다.
실제 식을 점화하면 수많은 재귀호출이 일어날 것이다. 도시의 개수(N)이 10개라고 하자. 이때 \(find\_path(1, 2, \{1, 3, 2\})\), \(find\_path(1, 3, \{1, 2, 3\})\)가 호출되었을 때 각 함수는 모두 \(find\_path(1, 4, \{1, 2, 3, 4\})\)을 호출한다. 확실히 중복이 발생했다. 2장 1절에서 \(V\)의 구체적인 경로는 중요하지 않다는 것을 확인했다. \(\{1, 2, 3\}, \{1, 3, 2\}\)는 구분할 이유가 없다. 중요한 것은 방문했는지, 안 했는지의 여부뿐이다.
좋아, 중복 여부도 확인했으니 동적 계획법을 위한 캐시의 크기를 산정하면 된다. 현재 세 개의 변수를 사용하는데 start, last는 도시의 수 \(N\)을 따라가고, 방문 여부 집합은 방문 여부 0과 1을 담기 때문에 \(2^N\)개의 상태를 가질 수 있다. 그러면 캐시의 크기는 \(N*N*2^N = N^{2} 2^N\)라는 것을 확인할 수 있다. 동적 계획법에서는 알고리즘의 시간복잡도가 캐시의 크기를 따라가기 때문에 시간복잡도는 곧 \(O(N^{2} \times 2^N)\)가 된다.
하지만, 마지막 통찰을 통해 이를 한 번 더 개선할 수 있다.
2.3. 시작 도시도 중요하지 않다
이전 절에서 중간 경로의 구체적인 순서는 중요하지 않고, 특정 세 변수값에 대해 중복 호출이 일어난다는 것까지 확인했다. 그리고 이를 통해 우리는 완전탐색의 \(O(N!)\)의 시간복잡도를 \(O(N^{2} \times 2^N)\)까지 끌어내릴 수 있는 기반을 마련했다. 하지만 마지막 통찰을 통해 시간복잡도를 한 번 더 낮출 수 있다. 이는 원 문제에서 간략하게 설정한 중요한 조건에 기반한다.
한 번 방문한 도시는 재방문하지 않는다.
일견으로는 참 사소하다 싶다. 그러면 이 원칙을 지키면서 만든 완전한 하나의 경로를 살펴보자.
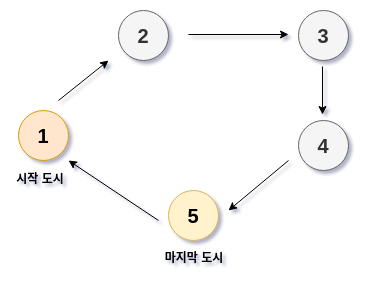
도시의 개수가 5개일 때 문제의 답이 될 수도 있는 하나의 경로이다. 1번 도시에서 시작하고 5번 도시에서 여행을 마치고 1번 도시로 오는 것을 확인할 수 있다. 이 경로가 문제에서 원한 답이라고 하자. 이 경로에서 여행 비용이 최소가 된다.
이때 한 번 방문한 도시는 재방문하지 않고, 여행을 마치고 시작 도시로 돌아오기 때문에 이 경로는 결국 사이클(cycle)임을 알 수 있다. 사이클은 그래프에서 매우 중요한 개념 중 하나로 일반적인 개념으로는 첫 정점과 마지막 정점이 중복되는 경로로 이를 통해 경로를 무한히 순회할 수 있다.
모든 정답 후보군을 구성하는 경로가 사이클인 것이 중요한 이유는 이 경로를 만들 수만 있으면 시작점은 중요하지 않기 때문이다. 즉, 1번에서 시작하든, 2, 3, 5번에서 시작하든 정답 경로는 반드시 훑게 되어 있고, 결국 시작점을 단일 도시로 고정해도 정답 경로를 지나치게 돼서 시작 도시를 추적하지 않아도 된다. 이를 통해 우리가 관리해야 할 변수는 3개에서 2개가 된다. start 변수를 생략하자!
이 통찰을 통해서 우리는 여행 시작 도시를 생략할 수 있으므로 시간 복잡도는 한 번 더 개선되어 \(O(N \times 2^N)\)가 된다. \(N\)만큼이 더 줄어든 것을 확인할 수 있다.
이 세 가지 통찰을 바탕으로 실제 동적 계획법 코드로 넘어가자.
3. 실제 코드
2장에서 동적 계획법으로 코드를 개선하기 위해 필요한 세 가지 통찰을 확인했다. 이제 실제 코드를 살펴보자. 더 유려해진 것을 확인할 수 있다.
def tsp(dists):
N = len(dists)
VISITED_ALL = (1 << N) - 1
cache = [[None] * (1 << N) for _ in range(N)]
INF = float('inf')
def find_path(last, visited):
if visited == VISITED_ALL:
return dists[last][0] or INF
if cache[last][visited] is not None:
return cache[last][visited]
tmp = INF
for city in range(N):
if visited & (1 << city) == 0 and dists[last][city] != 0:
tmp = min(tmp,
find_path(city, visited | (1 << city)) + dists[last][city])
cache[last][visited] = tmp
return tmp
return find_path(0, 1 << 0)
코드의 중요한 부분을 설명하면 다음과 같다.
cache = [[None] * (1 << N) for _ in range(N)]
동적 계획법을 위한 캐시를 초기화한다. range(N) 을 통해 도시의 개수(N)에 대응하고 (1 << N) 을 통해 방문한 도시 집합(V)에 대응한다. 만약 start 변수까지 추적해야 했다면 캐시의 차원이 한 단계 더 증가해 복잡해졌을 것이다. 하지만 이제는 그러지 않아도 된다. 각 셀의 초기값은 None 으로 둔다.
if visited == VISITED_ALL:
return dists[last][0] or INF
완전탐색 코드에서 모든 도시를 방문했을 때와 유사하다. 하지만 조금 다른데 이번에는 or 연산자를 썼다. 이 연산자를 통해 마지막 방문 도시와 0번째(여기서는 시작 도시) 사이의 경로가 존재하면(이 문제에서는 값이 0이 아니라면) 이 경로 값을 반환하고 이어져 있지 않다면(이 문제에서는 값이 0이라면) 무한값을 반환해서 절대 답이 될 수 없게 한다.
if cache[last][visited] is not None:
return cache[last][visited]
우리는 캐시의 초기값을 None 으로 했다. 근데 값이 None 이 아니라는 얘기는 해당 last 와 V 에 대한 계산이 이미 이루어졌고 지금은 중복 호출되었다는 뜻이기 때문에 다시 재계산하지 않고 값을 바로 반환한다. 동적 계획법은 이렇게 중복 계산을 없애 효율을 높인다.
tmp = INF
for city in range(N):
if visited & (1 << city) == 0 and dists[last][city] != 0:
tmp = min(
tmp,
find_path(city, visited | (1 << city)) + dists[last][city]
)
cache[last][visited] = tmp
이제 첫 계산이라면, 방문하지 않은 모든 도시를 모두 방문해서 그중 최소값을 선택해야 한다. 그래서 tmp 를 무한으로 설정하고, 방문하지 않은 도시를 각각 방문하고 tmp 를 점점 줄여나간다.
tmp 의 최소값을 경신하는 식의 find_path 재귀호출에서 dists[last][city] 를 더해나가는 것을 확인하자. tmp_dist 를 함수에 인자로 넣는 대신 이렇게 더하는 방식을 통해서도 값을 구할 수 있다. 이는 사실 완전탐색 식에서도 마찬가지다. 이전 포스트에서 이렇게 하지 않은 이유는 처음 떠오른 방식이 인자로 값을 넘기는 방식이었기 때문이다. 하지만 확인 결과 꼭 그러지 않아도 충분했다.
모든 도시를 방문하고 최소로 경신된 tmp 를 캐시에 저장한다. 이후 이 last, V 에 대한 호출에서는 재계산하지 않고 바로 답을 반환할 수 있다.
return find_path(0, 1 << 0)
점화식을 ignite한다. 2장 3절에서 시작 도시는 어디가 되어도 결국 정답 경로를 찾게 된다는 것을 확인했다. 그래서 여기서는 0번 인덱스의 도시를 시작 도시로 고정하고 여행을 시작한다. 하지만 시작 도시는 1, 2, …, \(N\)-1번 도시가 되어도 관련 코드만 수정해주면 답이 나올 것이다. 그렇기에 추적하지 않는 것이다!
이렇게 동적 계획법을 통해 TSP를 해결해보았다.
4. 마치며
결국에는 이 포스트를 완성했다. 이 동적 계획법 포스트는 나한테는 도전이었다. 문제 자체가 까다로워서 사실 어떻게 포스트를 진행해 나가야 할지 감이 오지 않았기 때문이다. 아마 지금까지 다룬 알고리즘 포스트 중에는 가장 까다롭지 않았을까? 부족한 부분이 있겠지마는 일단은 후련하다.
첫 연속 포스트를 일단락지었다. TSP의 다양한 알고리즘 중 가장 잘 알려진 동적 계획법까지만 다뤘기 때문에 다른 방법론에 대해 언젠가 다루지 말라는 법은 없지만 현재는 잘 모르겠다. 아직 내게 미개척지로 남은 분야가 너무 많아서… 하지만 두고 볼 일이다.
포스트를 2주만에 작성했다. 뭐 일하면서 바빴다고 말하고 싶지만 결국 변명이라는 것을 안다. 다음주에는 미루지 않고 꼭 하나라도 작성할 수 있도록 해봐야겠다.
이상 포스트를 마칩니다.
