숫자 배열에서 두 번째로 큰 값 찾기

숫자 배열에서 두 번째로 큰 값 찾기

2019, Sep 11    

0. Index

  1. 들어가며
  2. Way 1: 정렬하기
  3. Way 2: for문 한 번에 끝내기
  4. 그게 최선입니까? 확실해요?
  5. 마치며


1. 들어가며

재미있는 알고리즘 문제를 들고 왔다. 바로 숫자 배열에서 두 번째로 큰 값 찾기. 파이썬에서 배열의 최대값을 찾는 것은 매우 간단하다. 누구나 알 듯이 max 함수를 쓰면 되는데, 그러면 두 번째로 큰 값은 어떻게 찾을까? 딱히 생각을 하지 않으면 그 누구도 이런 질문을 하지 않는다. 1등만 기억하는 더러운 세상.

문제가 너무 직관적이고 쉬워서 따로 ‘문제 소개’ 장은 넣지 않고 바로 알고리즘으로 넘어간다. 두 번째로 큰 값을 찾는 알고리즘을 두 개 가져왔다. 하나는 너무 쉽고, 다른 하나는 약간의 사고를 해야 한다. 후자의 방법이 시간복잡도가 더 좋기 때문에 기억할만한 가치가 있다.

그 다음 여기서 끝내기에는 뭔가 아쉽다. 그래서 문제를 확장해서 생각하고 핵심 아이디어를 도출해 더 범용적인 기능을 만들어보는 것까지 진행해본다.

아 참고로, 내 코드에서는 값이 중복되어 같은 경우는 포함하지 않는다. 예를 들어 [2, 2, 1] 에서 중복을 허용하면 두 번째로 큰 값은 2가 되지만 우리는 허용하지 않는다. 따라서 답은 1이 된다.



2. Way 1: 정렬하기

가장 쉬운 방법은 역시 정렬을 통한 방법이다. 배열을 내림차순 정렬하고 두 번째로 발견되는 고유한 값을 반환하면 그대로 된다.

def second_largest_number(arr):
    unique_nums = set(arr)
    sorted_nums = sorted(unique_nums, reverse=True)
    return sorted_nums[1]

배열의 두 번째 큰 값인 second_largest_number 함수를 정의했다. 이때 set 을 통해 정렬 전에 고유한 값만 남기는 작업을 첫째 줄에서 진행하는데 우리는 중복을 허용하지 않기 때문에 이 작업을 거쳐야 한다. 그후 내림차순 정렬하고, 2번째 값을 반환하면 된다.

무식하게 쉬운데 이건 맛보기다. 시간복잡도는 정렬을 사용하기 때문에 \(O(N log N)\)이 된다.



3. Way 2: for문 한 번에 끝내기

이 방법이 아마 이 포스트를 읽는 사람들이 만족해하지 않을까 싶다. 앞선 정렬방법은 시간복잡도가 \(O(N log N)\)였는데, 좀 더 잘한다면 반복문 한 번으로 끝낼 수 있다.

핵심은 최대값과 두 번째 큰 값을 추적하는 변수를 두고, 배열의 각 값을 순회하며 두 변수를 갱신하는 것이다. 알고리즘이 어렵지는 않기 때문에 바로 코드를 확인하자.

def second_largest_number(arr):
    second = largest = -float('inf') 
    
    for n in arr:
        if n > largest:
            second = largest
            largest = n
        elif second < n < largest:
            second = n

    return second

앞선 함수와 같은 이름의 함수지만 이번에는 반복문 한 번에 해결할 수 있었다. 중요한 각 부분을 설명하면 다음과 같다.

second = largest = -float('inf')

최대값과 두 번째 큰 값을 추적할 변수 largest, second 변수를 음의 무한으로 초기화한다. 이 값을 음의 무한대로 초기화한 것은 중요한 의미가 있는데, 우리는 for 반복문을 돌면서 두 변수를 점차 큰 값으로 깎아 나갈 것이기 때문에 그를 위해서는 값을 가장 작은 값으로 만들어놔야 한다. 종종 충분히 작은 값으로 초기화해야 할 때 -99999999, 이런 식의 값을 쓰는 경우가 있는데 이런 경우는 피해야 한다. 배열의 최대값이 저 은하철도 999 숫자보다 작은 경우가 얼마든지 있을 수 있으니까.

for n in arr:
    if n > largest:
        second = largest
        largest = n
    elif second < n < largest:
        second = n

다음은 실제로 반복문을 돌면서 두 번째로 큰 값을 만들어나가는 과정이다. 현재 순회하는 배열의 값 n 에 대해 우리가 생각해봐야 할 케이스는 3가지다.

  1. 현재 최대값(largest)보다 클 경우:
    • 최대값과 두 번째 큰 값 모두 경신하면 된다. 먼저 두 번째 값을 이전 최대값으로 재설정하고, 최대값에 n 을 둔다.
  2. 두 번째 큰 값보다 크고 최대값보다 작은 경우:
    • 두 번째 값(second)만 경신하면 된다.
  3. 그 외:
    • 무시한다. 난 나보다 약한 상대의 말 따위는 듣지 않는다.

저 반복문 코드는 정확히 이 세 상황에 대응한다.


이 코드는 \(O(N)\)의 준수한 시간복잡도로 문제를 정확하게 해결하며 정렬 코드에 비해 그렇게 복잡하지도 않다. 그래서 이 문제에 대한 더 바람직한 해결책이라고 할 수 있겠다. 우리는 이제 2등도 기억할 수 있게 됐다.

이상 포스트를 마칩니다.



4. 그게 최선입니까? 확실해요?

물론! 겨우 이 정도로 끝나지 않았다. 겨우 이 정도의 분량과 인사이트를 가진 포스트를 내가 굳이 만들지는 않으니까. 이 포스트를 만든 이유에 대한 구현은 지금부터다.

이번 문제는 숫자 배열에서 두 번째로 큰 고유한 값을 찾는 것이었다. 하지만 이 정도에 만족하면 성장하지 않는다. 더 생각해볼 것은 없을까?


4.1. 확장의 여지

항상 이야기하지만 좋은 프로그램이란 무엇인가란 질문을 끊임없이 해야 한다. 이 질문은 정말 어려운 질문이지만, 이 두 명제는 많은 경우 참인 것 같다.

1. 좋은 프로그램은 많은 사람들이 쓰는 프로그램이다.
2. 많은 사람들이 쓰면 좋은 프로그램이 된다.

꼬리에 꼬리를 무는 느낌인데 이 두 명제는 서로 상호보완적이다. 좋은 프로그램은 당연히 그렇지 않은 프로그램보다 많은 사람들이 쓸테고, 또 많은 사람들이 쓰다보면 사용자 정보 축적 등 다양한 이유로 더 좋은 프로그램이 될 수 있다. 카카오톡이 라인보다 정말 압도적으로 우월해서 다수의 대한민국 국민들이 일상 메신저로 쓰는걸까? 난 아니라고 본다.


돌아와서, 좋은 프로그램은 많은 사람들이 쓰는 프로그램이다. 이때 분명히 해야 할 것은 사용자마다의 요구사항이나 수요가 다 다를 것이라는 것이다. 다시 말해 좋은 프로그램은 다양한 수요와 니즈를 갖춘 사용자를 모두 만족시킬 수 있는 프로그램을 말한다.

이때 우리 프로그램은 좋은 프로그램일까? 우리 프로그램의 문제의식은 배열의 최대값이 아닌 두 번째로 큰 값을 찾는 것이다. 그러면 경우에 따라선 세 번째 값이나 네 번째 값, 100번째 큰 값을 원하는 사람은 정말 없을까??? 두 번째 큰 값을 찾는 사람뿐 아니라 다른 사람들의 수요도 만족시킬 수 있다면, 보다 범용적인 프로그램이라면 더 많은 사용자를 만족시킬 수 있고, 더 좋은 프로그램일 것이다.

따라서 단순히 이 문제를 구현함을 넘어 우리는 확장의 여지를 본다.

숫자 배열에서 K번째로 큰 고유한 값을 찾아라

우리의 문제는 보다 일반적이 되었으며 문제를 해결해 탄생하는 기능은 아마 더 범용적인 기능이 될 것이다.


4.2. 핵심 아이디어: 삽입정렬

좋다. 확장된 문제를 구현하자. 어떻게 해야 할까? 우리는 포스트에서 두 가지 방법을 살폈는데 먼저 정렬의 경우 이 문제를 구현하는 것은 매우 쉽다. 원 코드에서는 반환값에서 두 번째를 의미하는 1을 인덱스로 했는데 그 대신 새로 받은 K-1번째 값을 반환하면 된다. 코드는 대략 이렇게 된다.

def kth_largest_number(arr, K):
    unique_nums = set(arr)
    sorted_nums = sorted(unique_nums, reverse=True)
    return sorted_nums[K-1]

함수의 이름의 접두사를 second 가 아닌 K번째를 의미하는 kth 로 변경했다. 그리고 사용자가 원하는 순서를 뜻하는 K 인자를 받는다. 코드는 두 번째 큰 값을 찾던 원래 코드와 거의 일치하며, 반환할 때만 인덱스를 K-1 로 하면 된다.


정렬의 경우는 쉬웠는데 두 번째 알고리즘은 까다롭다. 가령 K가 100이라고 해보자. 어떻게 100번째 값을 저장해야 하는가. 원 코드를 참조해 첫 번째, 두 번째, 세 번째, …, 100번째 큰 값을 담는 100개의 변수를 설정해야 할까?

이 경우에는 배열에 최대값부터 K번째까지의 값을 저장하는 것이 바람직해보인다. 애초에 그럴 용도로 배열을 쓰는거니까. 이 방법이 K개의 줄에 변수 할당식을 쓰는 방법보다 훨신 유용해보인다. 이 포스트에서는 이 용도의 배열을 memory라고 표현하겠다.


그 다음으로, 반복문의 한 번의 순회에서 어떻게 if 문을 써나가야 할까? 아까 K가 2개인 경우에 우리가 상정해야 할 케이스가 3가지였다. 그러면 K에 대해서는 K+1 가지의 케이스를 고려해야 한다는 것인데.

이 경우에도 memory를 반복문으로 순회하며 새로운 값을 뒤집어써야 할 경우에 값을 재설정하면 될 것 같다.


마지막으로 하나 더 고려해야 한다. 원 배열을 순회할 때 K개의 값을 갖는 memory에 첫 번째부터 K번째 큰 값까지 유지·변경할텐데 이 과정을 어떻게 해야 할까? 가령 K가 5고 배열 순회 중 세 번째 큰 값보다 큰 새로운 값을 찾았을 때 어떻게 이를 기록할까?

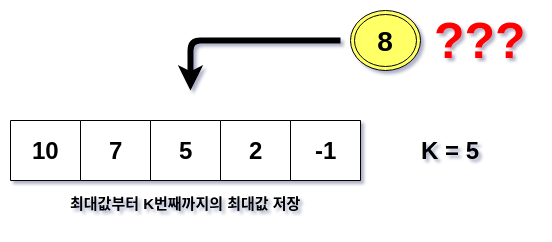
how_to_insert_kth_largest

힌트는 아까 만든 두 번째 큰 값을 찾는 코드의 비교 부분을 보면 된다.

    for n in arr:
        if n > largest:
            second = largest
            largest = n

정확히 필요한 부분만 가져왔다. 만약 지금 순회하는 배열의 값 n 이 가장 큰 값(largest)보다 클 경우 largest 를 바로 n 으로 할당하는 것이 아니라, 두 번째 값을 largest 으로 재설정한 뒤, largest 값을 n 으로 뒀다.

이것을 현재 문제로 확장하면 현재 배열의 값(n)보다 작은 값을 찾으면 그 뒤의 원소들을 모두 한 번씩 뒤로 물린 뒤에 그 위치에 n 을 두는 것이 핵심이다.

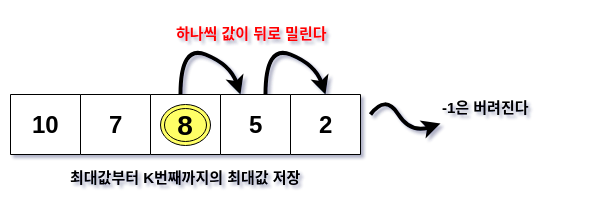
inserted numbers

이는 흡사 삽입정렬(insertion sort)을 연상시킨다. 삽입정렬에서도 오름차순일 때 현재 값보다 작은 값을 찾으면 뒤의 나머지 값을 모두 하나씩 뒤로 미룬 뒤에 값을 할당했으니까. 이제 이 핵심개념을 토대로 실제 코드를 작성해보자.


4.3. 실제 코드

def kth_biggest(arr, K):
    """숫자 배열에서 K번째로 큰 값을 구한다.

    이 함수는 고유한 값을 대상으로 한다.
    가령 [2, 2, 1]에서 2번째로 큰 값은 2가 아닌 1이다.

    또한 K가 배열의 고유한 값들의 개수보다 크면 IndexError를 반환한다.

    :input:
      arr | list := 숫자 배열
      K   | int  := 1 이상의 정수를 대상으로 한다.

    :return:
      int := 배열에서 K번째로 큰 값
    """
    # 예외 처리: K는 배열의 고유한 값 개수보다 클 수 없다.
    ORDINAL_MSG = ('st', 'nd', 'rd')[K-1] if K <= 3 else 'th'
    unique_set = set(arr)
    if len(unique_set) < K:
        raise IndexError(f"There's no {K}{ORDINAL_MSG} value in array")
    elif K <= 0 or not arr:
        raise ValueError("K should be over 0 and arr should not be empty")


    # 상수 및 변수 선언
    INF = float('inf')
    memory = [-INF] * K


    # 실제 검색 연산
    for n in arr:
        if n <= memory[-1]:
            continue

        for i, m in enumerate(memory):
            if (i == 0 and n > m) or m < n < memory[i-1]:
                for j in range(len(memory)-2, i-1, -1):
                    memory[j+1] = memory[j]
                memory[i] = n
                break

    return memory[-1]

실제 코드를 만들었다. 이 부분이 이 포스트에서 제일 중요해서 docstring과 에러체크하는 부분까지 다 넣어 완전한 기능으로 완성했는데 중요한 각 부분을 확인하면 다음과 같다.

# 예외 처리: K는 배열의 고유한 값 개수보다 클 수 없다.
ORDINAL_MSG = ('st', 'nd', 'rd')[K-1] if K <= 3 else 'th'
unique_set = set(arr)
if len(unique_set) < K:
    raise IndexError(f"There's no {K}{ORDINAL_MSG} value in array")
elif K <= 0 or not arr:
    raise ValueError("K should be over 0 and arr should not be empty")

실제 코드를 작성하기 전에 arr, K 가 올바른 값인지 확인하는 과정을 거쳤다. 정상적으로 기능이 작동하기 위해서는 arr 은 비어있으면 안 되고, K 는 1 이상의 정수여야 하며, arr 의 고유한 값의 개수(데이터베이스 용어로는 ‘cardinality’)보다 커서는 안 된다. 이 조건을 검증했다.

주석 바로 위의 줄은 개인적인 욕심으로 적었는데 고유한 값의 개수가 K 보다 작을 경우 “There’s no 1st value..” 와 같은 메시지를 넣고 싶었다. 그런데 서수 표현에서 숫자에 따라 뒤에 붙는 기호가 ‘st’, ‘nd’, ‘rd’, ‘th’와 같이 변하기 때문에 이를 위한 코드를 넣었다. 중요하지는 않으니 넘어가자.


# 상수 및 변수 선언
INF = float('inf')
memory = [-INF] * K

첫 번째부터 K번째 큰 값까지 저장할 memory 를 선언했다. 크기는 당연히 K 인데, 각 값을 음의 무한대로 초기화한 것을 눈여겨볼만하다. 여기에는 최대값 이하 숫자들이 들어갈 것이기 때문에 가급적 최소값으로 해놓으면 무리없이 각 원소가 채워질 것이다.


for n in arr:
    if n <= memory[-1]:
        continue

배열의 원소마다 순회한다. 각 숫자로 실질적인 알고리즘을 진행하기 전에 먼저 이 숫자와 현재 memory 의 K번째 값과의 대소관계를 비교한다. 이 이유는 현재 n 이 지금까지의 memory의 최소값보다 작거나 같으면 밑에 중첩된 반복문 자체를 실행하지 않아도 되기 때문이다. 따라서 이 경우에는 continue 로 건너 뛴다. 이제 핵심 부분으로 넘어가자.

    for n in arr:
        for i, m in enumerate(memory):
            if (i == 0 and n > m) or m < n < memory[i-1]:
                for j in range(len(memory)-2, i-1, -1):
                    memory[j+1] = memory[j]
                memory[i] = n
                break

    return memory[-1]

n 과 memory의 각 값을 비교하기 위해 for 문을 중첩했다. 이때 n 과 현재 비교하는 memory 의 값을 m 이라고 할 때, n 이 memory 에 들어오기 위해서는 n 은 m 보다 커야하고 m 의 바로 앞의 값보다는 작아야 한다. 그 검증을 if 문에서 하고 있다. 단, m 이 첫 번째 원소라면 m 의 바로 앞의 값은 없기 때문에 i가 0일 때는 따로 검증해 or로 묶는다. 이렇게 하지 않으면 memory[i-1] 부분에서 ‘-1’이라는 엉뚱한 인덱스가 튀어나올 수 있다.

만약 조건식에서 True가 반환된다면, 다시 말해 n 이 값을 뒤집어써야 할 m 과 그 위치를 찾았다면 다시 한 번 반복문을 실행한다. 값을 하나씩 뒤로 밀어야하기 때문이다. 이때 현재 m 의 위치 i 가 아니라 맨 뒤에서부터 거꾸로 앞의 값을 현재 위치로 뒤집어써야 한다는 것을 명심하자. 두 번째 큰 값을 찾는 코드에서도 n 이 largest 보다 클 때 largest 보다 second 변수가 먼저 재설정됐다는 것을 보면 납득할 수 있다.

현재 m 의 위치 i 의 바로 뒤까지 값이 밀렸으면 이제 i 에 n 을 할당한다. 그러면 현재까지의 최대값이 경신된다.

반복문을 완전히 탈출한 뒤에 memory의 마지막 값이 K번째 최대값이기 때문에 이를 반환하면 된다.


4.4. 시간복잡도 비교

두 코드의 시간복잡도는 어떻게 될까? 일단 정렬코드는 여전히 \(O(N log N)\)이다. 문제는 뒤의 코드인데 두 번째 큰 값을 찾을 때는 \(O(N)\)이라고 할 수 있었으나 지금은 다르다. K의 값이 미지수이기 때문이다. 복잡도는 for문을 보면 이해할 수 있는데 원 배열(\(N\))에서 memory와 관련된 두 번의 for문이 연속적으로 중첩된다. 따라서 이 코드의 복잡도는 \(O(N * K^2)\)가 된다.

생각보다 복잡도가 높아서 이 코드가 정렬보다 무조건 좋다고는 말할 수 없다. K가 2, 3과 같이 충분히 작다면 효율적이겠지만 가령 1000번째 큰 수를 찾는다고 하면 매우 복잡해진다.

사실은 포스트를 기획했을 때는 대충 계산해서 복잡도를 \(O(N * K)\)로 추정했다. 하지만 지금 보니 아니여서 조금 당황했는데 그래도 K가 (충분히) 작을 때는 유의미하다고 생각한다. 문제상황에 맞게 필요한 방법을 사용하면 되겠다.



5. 마치며

현재 나는 초심자분들과 알고리즘 스터디를 하며 그분들의 코드에 리뷰를 많이 한다. 이 문제도 같이 풀고 코드를 받았는데, 이 문제에 대해 가장 쉬운 접근법으로 풀지 않는 분들이 꽤 있다. 역시 처음엔 다 어려운 법이다. 그런 의미에서 이 문제를 포스트 주제로 잡은 것은 나쁜 선택은 아닌 것 같다.

다만 다루는 문제가 점점 쉬워지는 것은 아닌가 하는 생각도 들기는 하는데 결국 중요한 것은 내 컨셉인 것 같다. 내 알고리즘 포스트의 핵심컨셉은 한 문제를 위한 알고리즘은 여러 가지일 수 있다이기 때문에 이를 증명하는 다양한 수준과 복잡도의 알고리즘을 제시하는 것이 중요하겠다.

다음엔 어떤 포스트를 해야 할까? 벌써부터 마감의 압박이 느껴진다.

이상 포스트를 마칩니다.

Twitter Facebook Google+
# second_largest_number # kth_largest_number