![[Python] 2차원 배열 회전 알고리즘](/assets/img//algorithm/2d-array-rotation-logo.jpg)
[Python] 2차원 배열 회전 알고리즘
0. 목차
- 들어가며
- 문제 소개
- 알고리즘!
- 3.1. 90도 회전
- 3.2. 180도 회전
- 3.3. 270도 회전
- 3.4. 전체 함수 작성하기
- 마치며
1. 들어가며
전에 1차원 배열을 회전하는 알고리즘에 대해 다뤘다. 여기에서 다양한 알고리즘을 많이 다뤘는데(5개면 많은거지?) 마음 한켠으로는 달갑지 않았다. 왜냐하면 이 포스트는 ‘한 문제를 해결하는 다양한 방법을 알면 좋다‘는 내 철학에는 부합했지만 문제 자체가 정말 의미가 있는지는 진심으로 다가오지 않았기 때문이다. 현실에서 1차원 배열을 회전하는 수요가 많이 있나? 맨 앞에 있던 사람이 맨 뒤로 가는 회전하는 대기열이라든지.. 잘 모르겠다.
하지만 2차원 배열 알고리즘의 회전은 수요가 확실하고 우리에게도 매우 친숙하다. 이미지 90도 회전, 분명 많이들 해봤으리라 생각한다.(마우스로든, 손가락으로든) 난 현실적인 수요에서 가장 중요한 배열 회전 알고리즘은 2차원이라고 생각했고, 따라서 이번 포스트에서는 2차원 배열을 회전하는 방법에 대해 다룬다.
참고로 회전 코드로 바로 이동하려면 3장 4절로 넘어가면 된다.(‘CTRL + F’로 ‘3.4.’ 검색)
2. 문제 소개
문제는 1장에서 다 이야기했다. 2차원 배열(행렬)을 회전하는 것. 90도 단위씩 오른쪽으로 회전하며 이때 \(4n\)번(360도) 회전하면 원 배열과 결과값이 같아진다. 이를 그림으로 표현하면 다음과 같다.
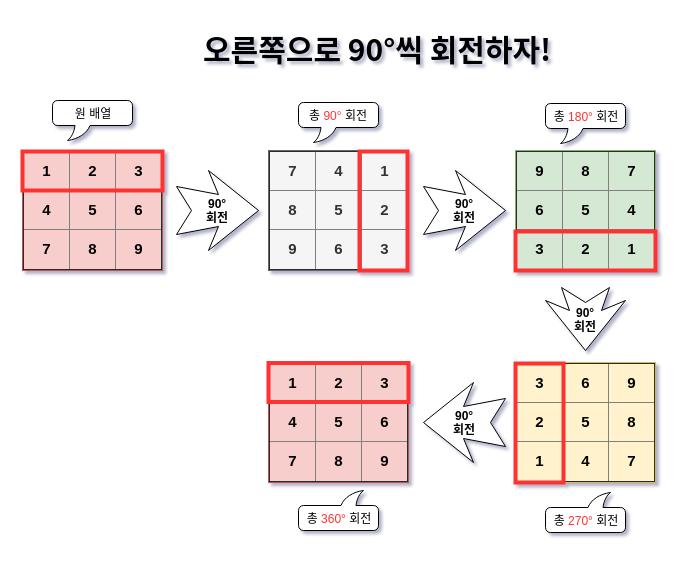
회전 방향을 좀더 보기 쉽게 [1, 2, 3]을 빨간색으로 하이라이팅했다. 이후 이 행을 기준으로 알고리즘을 만들 것이다. 이번 포스트는 이와 같이 2차원 배열을 회전하는 알고리즘을 구현한다.
이번 포스트에서는 원 배열은 행과 열의 수가 같은 정방형 배열(square array 또는 square matrix)이라고 가정한다. 행과 열의 수가 다를 때에는 조금 더 생각해야겠지만 핵심 아이디어는 같다.
알고리즘을 살펴보자.
3. 알고리즘!
2차원 배열은 90도 단위로 회전한다. 90도, 180도, 270도, 360도… 360도 회전한 결과는 원 배열과 같으며 이후에는 이 4개의 형태를 반복한다. 따라서 각 회전을 구현할 생각이다. 360도는 자기 자신이기 때문에 사실 하지 않아도 된다. 따라서 3개의 회전 알고리즘을 구현 후 템플릿 함수에 담으면 될 듯 싶다.
180도, 270도 회전은 90도 회전을 작성 후 2번, 3번 반복하면 되지 않냐고 물을 수 있다. 물론 맞지만, 이 중복이 싫기도 하고 두 구현이 결코 어렵지도 않다. 그러니 90도 회전을 반복해서 사용하지는 않고 각각 다른 코드로 만들겠다.
각 알고리즘은 원 배열에 변화를 주지 않고, 회전된 새 배열을 만들어서 이를 반환하는 것으로 한다. 이는 360도일 때도 마찬가지이다.
3.1. 90도 회전
아까의 예제에서 오른쪽으로 90도 회전한 결과만 따로 놓고 보자.
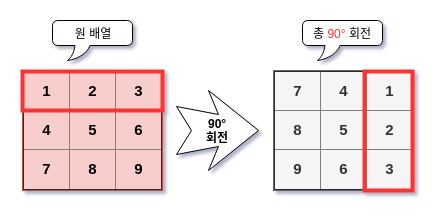
이것을 어떻게 알고리즘으로 구현해야 할까? 배열의 행과 열을 나타내는 for 문을 중첩하면 될 것 같긴한데 한눈에 잡히진 않는다.(적어도 나는 그렇다) 그래서 일부러 [1, 2, 3] 이 첫 행을 하이라이팅했다. 이 행이 어떻게 변화하는지 살펴보고 나머지에 모두 적용하면 된다.
저 박스 안의 숫자가 어떻게 변화하고 있는가? 너무 어렵게 생각하지 말자. 1, 2, 3, 각 숫자가 위치하는 셀의 행과 열이 어떻게 변화하고 있는지 보자.
| N | Before | After |
|---|---|---|
| 1 | (0, 0) | (0, 2) |
| 2 | (0, 1) | (1, 2) |
| 3 | (0, 2) | (2, 2) |
원 배열의 [1, 2, 3]과 회전 후의 [1, 2, 3]의 행, 열 번호를 튜플로 나타냈다. Before는 회전 전의 위치고, After는 회전 후의 위치를 나타낸다.
각 상태의 행과 열을 기준으로 살펴보자. 여기서 규칙성이 보인다.
회전 전의 열 번호와 회전 후의 행 번호가 일치한다.
그리고 회전 후의 열은 N-1 에서 회전 전의 행을 뺀 값과 같다.
여기서 2는 무엇인가? 현재 배열의 행과 열의 크기는 3(N)이다. 거기서 1을 뺀 숫자와 일치한다.(N-1) 왜 1을 빼줘야 할까?
0에서 3을 그대로 넣으면 IndexError가 발생하기 때문이다.
이제 우리가 할 일은 단서를 이용해 원 배열의 값을 반환할 배열의 새로운 위치에 복사하는 일이다. 코드로 보자.
def rotate_90(m):
N = len(m)
ret = [[0] * N for _ in range(N)]
# 왜 'ret = [[0] * N] * N'과 같이 하지 않는지 헷갈리시면 연락주세요.
for r in range(N):
for c in range(N):
ret[c][N-1-r] = m[r][c]
return ret
>>> test = [[1,2,3], [4,5,6], [7,8,9]]
>>> print(rotate_90(test))
[[7, 4, 1], [8, 5, 2], [9, 6, 3]] # OH yeah!!
입력 받은 2차원 원 배열은 m 이고, 반환할 배열은 ret 으로 정의한다. 배열의 행과 열의 크기는 N 이다. 우리는 입력이 정방형 행렬이라고 가정했기 때문에 N 으로 통일할 수 있다.
실제 복사 코드는 중첩된 for문 안에서 실행되는데 여기가 알고리즘의 핵심이다.
ret[c][N-1-r] = m[r][c]
아까의 단서에서 회전 전의 열과 후의 행이 일치한다고 했다. 따라서 두 곳에는 c 값을 그대로 준다.
다음으로 회전 후의 열은 N-1 에서 회전 전의 행을 뺀 값이라고 했다. 회전 전의 행 번호가 r 일 때, N-1(2)에서 r(0)값을 빼줌으로써 이 값을 만들 수 있다.
이 코드를 다른 행에 적용해보면 정확히 일치하는 것을 알 수 있다. 따라서 이 코드를 행렬의 모든 셀에 적용한다. 테스트도 올바르게 나온다.
3.2. 180도 회전
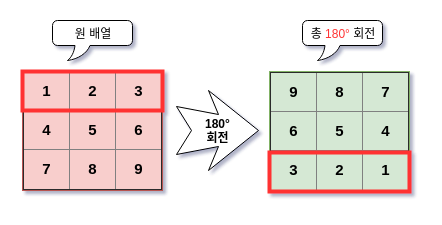
원 배열을 180도 회전했다. 확실히 뭔가 뒤집은 것 같기는 하다. 무언가가 평소의 모습과 완전히 상반되게 바뀐 것을 ‘180도 바꼈어!’라고 관용적으로 사용하는 것이 이제 이해가 된다.
[1, 2, 3]의 위치 변화를 살펴보자.
| N | Before | After |
|---|---|---|
| 1 | (0, 0) | (2, 2) |
| 2 | (0, 1) | (2, 1) |
| 3 | (0, 2) | (2, 0) |
규칙성이 보인다. 여기서는 전후의 행, 전후의 열이 서로 매칭되는 것을 발견할 수 있다.
회전 후의 행 번호는 N-1 의 값에서 전의 행 번호를 뺀 것과 같다.
회전 후의 열 번호는 N-1 의 값에서 전의 열 번호를 뺀 것과 같다.
좋아. 코드로 옮기자.
def rotate_180(m):
N = len(m)
ret = [[0] * N for _ in range(N)]
for r in range(N):
for c in range(N):
ret[N-1-r][N-1-c] = m[r][c]
return ret
>>> test = [[1,2,3], [4,5,6], [7,8,9]]
>>> print(rotate_180(test))
[[9, 8, 7], [6, 5, 4], [3, 2, 1]] # OH yeah!!
코드의 전반적인 모습은 아까와 동일한데, 값을 복사하는 이 한 줄만 다르다.
ret[N-1-r][N-1-c] = m[r][c]
이 코드는 발견한 규칙성을 그대로 반영한다.
180도도 해결되었다.
3.3. 270도 회전
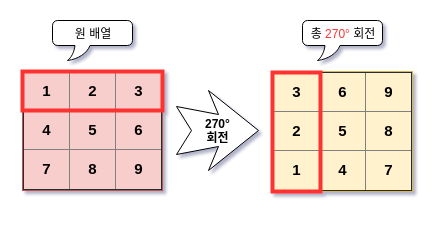
마지막 270도이다. 왼쪽으로 90도 회전했다고도 할 수 있다. [1, 2, 3]의 변화는 다음과 같다.
| N | Before | After |
|---|---|---|
| 1 | (0, 0) | (2, 0) |
| 2 | (0, 1) | (1, 0) |
| 3 | (0, 2) | (0, 0) |
회전 후의 열과 전의 행이 일치한다.
후의 행 번호는 N-1 에서 전의 열 번호를 뺀 값과 일치한다.
우리의 전제는 옳을까? 코드로 바로 옮겨보자.
def rotate_270(m):
N = len(m)
ret = [[0] * N for _ in range(N)]
for r in range(N):
for c in range(N):
ret[N-1-c][r] = m[r][c]
return ret
>>> test = [[1,2,3], [4,5,6], [7,8,9]]
>>> print(rotate_270(test))
[[3, 6, 9], [2, 5, 8], [1, 4, 7]] # OH yeah!!
기가 막히게도 들어맞는다.
이렇게 해서 90, 180, 270도 회전을 90도 회전을 반복하지 않고 구현해냈다.
3.4. 전체 함수 작성하기
이제 위의 함수들을 모아 사용자 원하는 만큼 회전하는 알고리즘을 작성하자.
이 함수는 원 배열 m 과 함께 몇 도 회전할지에 대한 입력도 받아야 한다.
그 입력을 90도를 한 단위로 하는 d 로 받자. 90도는 1, 180도는 2, 270도는 3, …
Help docs까지 추가해 완성한 최종 코드는 다음과 같다.
def rotate(m, d):
"""2차원 배열을 90도 단위로 회전해 반환한다.
이때 원 배열은 유지되며, 새로운 배열이 탄생한다. 이는 회전이 360도 단위일 때도 해당한다.
2차원 배열은 행과 열의 수가 같은 정방형 배열이어야 한다.
:input:
m: 회전하고자 하는 2차원 배열. 입력이 정방형 행렬이라고 가정한다.
d: 90도씩의 회전 단위. -1: -90도, 1: 90도, 2: 180도, ...
"""
N = len(m)
ret = [[0] * N for _ in range(N)]
if d % 4 == 1:
for r in range(N):
for c in range(N):
ret[c][N-1-r] = m[r][c]
elif d % 4 == 2:
for r in range(N):
for c in range(N):
ret[N-1-c][N-1-r] = m[r][c]
elif d % 4 == 3:
for r in range(N):
for c in range(N):
ret[N-1-c][r] = m[r][c]
else:
for r in range(N):
for c in range(N):
ret[r][c] = m[r][c]
return ret
이 함수는 아까 만든 세 함수의 짬뽕에 지나지 않는다. 다만 회전 단위 d 에 따라 분기만 할 뿐이다.
90도 회전은 1, 5, … 처럼 4로 나눈 나머지가 1,
180도 회전은 2, 6, … 처럼 4로 나눈 나머지가 2,
270도 회전은 3, 7, … 처럼 4로 나눈 나머지가 3,
360도 회전은 4, 8, … 처럼 4로 나눈 나머지가 0,
이 값에 맞게 분기 후 회전된 행렬을 반환한다.
4. 마치며
정방형 2차원 행렬을 90도 단위로 회전하는 알고리즘을 살펴보았다. 행렬과 관련한 알고리즘들은 항상 규칙성을 찾는 게 문제인 것 같다. 나도 처음에 바로 찾아내지 못하고 계속 고뇌했다.
이 알고리즘을 확장성 있게 하려면 결국 직사각형 행렬일 때까지로 넓혀야 한다. 그러면 회전 단위에 따라 반환되는 행렬의 크기가 달라지는 등 고려해야 할 점이 더 생긴다. 기회되면 그쪽까지 확장해서 이 포스트를 업데이트해도 괜찮겠다는 생각이 든다. 일단 여기까지 온 것도 나쁘지 않기 때문에 오늘은 여기에서 마무리한다.
마음속 숙제를 마쳤습니다. 홀가분합니다.
이상 포스트를 마칩니다.
