내가 알고리즘 문제를 푸는 방법

• 본 포스트는 데스크탑에 최적화되어 있습니다.

0. Index

1. 들어가며
2. 예제: 숫자 야구
   • 2.1. 주제 소개
   • 2.2. 문제 정의
3. 어떻게 접근할까?
   • 3.0. 나만의 방식으로 문제 정리하기
   • 3.1. 알고리즘 선택: 입력의 크기를 바탕으로
   • 3.2. 문제 분해 및 조합
   • 3.3. 조합: 수식으로 정리
4. 실제 코드
5. 내 방식의 문제점
6. 마치며
7. 자료 출처

1. 들어가며

내 블로그는 여러 카테고리가 있는데 그중 가장 잘 읽히는 카테고리는 단연 알고리즘이다. 현재 주간 통계에서 페이지뷰 상위 10위 중 8개가 알고리즘 포스트다. 그 원인은 여러 가지가 있을 수 있겠는데 분석 없이는 모두 뇌피셜이기 때문에 넘어간다. 참고로 이번주 1등은 팩토리얼을 구하는 여러 방법을 다룬 포스트인데, 실제 개발에 별 도움이 안 되는 팩토리얼 포스트가 왜 1등인지는 잘 모르겠다. 학생분들의 성원이 큰 힘이 된 것이 아닌가 추측만할 뿐이다.

내 알고리즘 포스트의 컨셉은 확실하다. 알고리즘 플랫폼의 구체적인 문제를 일일이 소개하는 것이 아닌 보다 일반적인, 유명한 주제의 알고리즘을 다루며 가능하다면 다양한 시간복잡도의 알고리즘을 소개하는 것. 사실 이 방식은 단순히 플랫폼 문제의 정답코드를 소개하는 것에 비해 하나의 포스트에 시간이 많이 소모되고 주제 찾기가 까다로워서 지금도 고민인데, 그대신 하나하나 웹상에 등재될 때마다의 성취감은 더 크다. 일단은 이렇게 계속 가지 않을까 싶은데…

오늘은 알고리즘 소개보다는 내가 알고리즘 문제를 실제로 어떻게 접근하고 해결하는지, 나의 방법론을 소개하고자 한다. 최근 스터디를 하면서 문제를 읽은 후 설계하지 않고 코드를 작성하는 분들이 아직도 꽤 있다는 것을 알게 됐다. 이는 알고리즘을 가르치는 곳은 많아도 어떤 프로세스로 접근해야 하는지는 가르치는 곳이 많지 않아서인지도 모르겠다. 하지만 명심하자. 설계 없는 코드는 공허하다. 설계 없이 코딩하는 것은 문제 난이도를 스스로 더 높이는 것이기도 하고, 또 해결이 된다한들 최종 결과물인 코드의 가독성이 심히 저해되기 쉽다.

그래서 실제 예제 문제를 하나 가져와서 그 문제를 해결하는 나의 프로세스를 순차적으로 소개하고자 한다. 가져온 주제는 숫자 야구인데 이 주제를 통한 다양한 문제 버전이 있지만 여기서는 정보올림피아드 대회에 나왔던 문제를 풀어본다. 구체적인 문제 링크는 다음과 같다.

포스트의 구성은 다음과 같다:

• 먼저 문제를 소개한다. 이후 장에서는 이 문제를 해결하는 실제적인 나의 정리방식을 소개할 예정이기 때문에 문제는 꼭 이해하고 다음 장으로 넘어가자.
• 다음 장에서는 본격적으로 이 문제를 보고 내가 취한 접근법을 소개한다. 몇 개의 절로 이루어지는데 그 과정을 상세히 짚고 넘어갈 생각이다. 이미 이 장이 제일 길 것이다.
• 다음은 이 접근법을 적용한 코드를 확인한다. 설계가 적절하면 코드 부분에서 오래 고민할 것이 없다. 나의 방식이 적어도 이 문제에서는 유효하다는 것을 확인할 것이다.
• 마지막으로 내 방법론의 부족한 부분도 짧게 자평할 것이다.

이 방식은 나만의 방식이고 정답이 결코 아니다. 향후 서술하겠지만 부족한 부분이 있는 것도 사실이다. 개선할 부분이 있으면 적극적으로 댓글 달아주세요. 합리적이면 무슨 수를 써서라도 내 것으로 만들겠습니다.

시작합니다.

2. 예제: 숫자 야구

2.1. 주제 소개

숫자 야구는 기본적으로 숫자를 맞추는 게임이다. 문제를 내는 사람은 1부터 9까지의 서로 다른 숫자 세 개를 선택해 세 자리수를 만든다. 그리고 문제를 해결해야 하는 사람은 세 자리수를 제시하는데, 문제를 낸 사람은 자신이 만든 숫자와 제시받은 숫자를 비교해 서로 얼마나 유사한지에 대한 정보를 제공하며 그 규칙은 다음과 같다:

• 숫자를 맞추고 그 위치까지 맞췄다면 1S(Strike)
• 숫자를 맞췄지만 위치가 다르다면 1B(ball)
• 물론 무엇이 볼이고 스트라이크인지는 가르쳐주지 않는다.

예를 들어보자.

내가 문제를 내는 입장이고 나는 ‘456’를 선택했다. 456은 각 자리수가 동일한 등차로 순증가하는 세 자리수로 우리의 마음 한켠을 따뜻하게 하기 때문이다. 물론 이 따뜻함은 나만의 것이기 때문에 숫자는 상대방에게 공유하지 않는다. 숫자를 맞춰야 하는 입장에서는 가능한 숫자를 제시한다. 그러면 이 숫자와 원 숫자(456)를 비교해 ball과 strike 개수를 제시한다.

위의 그림이 몇 개의 예를 보여주고 있는데 두 숫자에서 공통된 숫자가 있고 그 위치까지 같으면 S(Strike), 위치는 다르지만 공통된 숫자가 있으면 B(ball)로 표현하고 있다. 이때 비교 결과가 3S가 되면 정답을 맞춘 것이다.

이때 알 수 있는 것은 비교 결과가 ‘2S 1B’은 나올 수 없다는 것이다. 조금만 생각해보면 알 수 있다.

참고로 이 게임을 영어로는 ‘bulls and cows’라고 한단다.

2.2. 문제 정의

위에서는 숫자 야구라는 주제를 살펴봤다. 이 주제로 만들 수 있는 문제는 정말 많겠지만 우리가 이번에 푸는 문제는 다음과 같다:

'추측한 세 자리 수와 그에 대한 B, S의 개수'의 목록이 주어질 때, 원 숫자가 될 수 있는 남은 숫자들의 개수를 구하라

예를 들어 추측한 숫자와 B, S의 개수가 다음과 같이 주어졌다고 하자.

• 123: 1S 1B
• 356: 1S
• 327: 2S
• 489: 1B

이때 만들 수 있는 세 자리 수에서 답이 될 수 있는 원 숫자는 324와 328, 두 개뿐이다.

문제가 주어졌다. 어디서부터 시작해야 할까?

3. 어떻게 접근할까?

문제를 이해했다. 실제 코딩 테스트라고 생각하자. 시간이 째깍째깍 흐르고 문제를 최대한 침착하게 다 읽었다. 지금부터 설명할 다음 네 가지 부분은 실제로 내가 어떤 문제를 풀든 문제가 지나치게 쉽지 않은 이상 항상 적용하려고 하는 방법론이다.

3.0. 나만의 방식으로 문제 정리하기

내가 문제를 푸는 플랫폼은 그때그때 다르다. 가령 baekjoon online judge를 활용할 수도, programmers나 codewars 등을 활용할 수도 있다. 이때 각 플래폼마다 문제를 소개하는 방식이나 페이지 레이아웃이 다 다르다. 단적으로 예를 들어 한국인들이 애용하는 baekjoon과 programmers에서 같은 문제를 다뤄도 페이지 양식은 완전히 다름을 확인할 수 있다. 백준 플랫폼은 요즘 알고리즘 사이트들과는 다르게 한 페이지에서 문제와 에디터를 동시에 제공하지 않는다.

그렇기 때문에 문제를 나만의 방식으로 정리하고 표현하는 것이 중요하다. 그러면 문제를 다시 읽거나 특정 조건을 쫓을 때 플랫폼에 구애받지 않고 평소 익숙하던 대로 빠르고 정확하게 원하는 바를 달성할 수 있다.

또 긴 문제를 잘 정리해놓으면 한눈에 보기 좋다는 장점도 있다. 이번 2020 카카오 블라인드 테스트 1번 문제를 보자. 문제가 별 것도 아닌데 열어보면 문제 설명은 스크롤이 꽤 긴 것을 확인할 수 있다. 이는 프로그래머스가 한 페이지에 에디터도 같이 제공해서 문제 소개 영역이 좁은 것도 있고, 문제 해결에 별 도움이 안 되는 쓸데없는 잡설 또는 noise도 많이 껴있기 때문이기도 하다. ‘“어피치”가 문자열 압축 알고리즘을 공부하고 있다’는 정보는 이 문제 해결과는 전혀 상관이 없음에도 길이가 50이나 된다. 길이가 아닌 용량을 따진다면 한글 글자가 UTF-8에서 3바이트임을 감안하면 매우 큰 정보 낭비를 하고 있다.

따라서 문제를 읽고 난 후 설계나 코드로 들어가기 전에 자신만의 방법으로 어떻게든 정리하는 것을 강력히 추천한다. 문제를 나만의 방식으로 정리하고, 필요없는 정보는 생략해 일목요연하게 볼 수 있도록 하자. 나같은 경우에는 노트에 한두 페이지에 걸쳐 정리하는 것을 좋아한다. 그리고 ‘문제 체계화’ 부분과 ‘핵심 아이디어 추출’ 등 크게 두 부분으로 나누어 정보를 기록한다. 이 문제에 대해 ‘문제 체계화’ 부분까지 작성한 결과는 다음과 같다:

먼저 맨 위에 정의된 문제를 한 문장으로 기술한다. 이때 문장은 가급적 설명을 위한 설명(‘어피치가 열심히 문자열을 공부한다…’) 등이 아닌, 보다 일반적이고 프로그래밍적으로 추상화된 형태로 기술한다. 지금 문장은 실패한 문제 기술이다. 별로 프로그래밍적으로 추상적이지도, 일반적이지도 않기 때문이다. 이는 순전히 내 실력 부족이 원인이다.

다음에 나는 ‘문제 체계화’를 ‘Systematize’라는 영역에 적는다. 체계는 ‘System’이라고 할 수 있는데 내가 어디서 얼핏 듣기에 시스템은 크게 ‘입력’, ‘출력’, ‘처리’로 정리할 수 있다고 들었다. 그렇게 생각해보면 이 세상 모든 것은 체계다. 내가 만드는 프로그램도 입출력, 처리가 가능한 시스템이고, 삼성전자 조직도 시스템이며, 인간도 하나의 시스템이다. 가령 인간은 시청후촉각 정보, 음식물 등의 입력을 받고 신체작용이 곧 처리이며, 말, 글, 배변 등의 출력을 한다. 이렇게 볼 때 인간이 시스템이 아니라고 보는 시각이 더 신기해진다. 이때 알 수 있는 것은 입출력 채널은 단일하지 않을 수는 있다.

따라서 풀어야 하는 문제도 시스템으로 구성한다. 문제의 입력과 출력을 정리하고, 문제의 주요 조건 등을 처리로 분류해 적는다. 이때 입출력, 처리는 다음과 같이 정의한다:

• 입력: 만들어야 하는 기능의 주요 변수명, 변수의 자료형, 최대길이 등의 기본 사항을 적는다. 특정 변수에 대해 나는 이 세 가지를 다음과 같은 형식으로 적는다.
  • 변수명 | 자료형 := 변수에 대한 소개. 이후 변수의 조건에 대한 수학적 표기
  • 예는 위에서 ‘records’ 변수에서 확인할 수 있다. 이때 수학적 표기를 최대한 활용하는데 | |는 어떤 집합의 길이를 표시하는데 쓰이고, \(\in\)은 특정 원소가 어떤 집합에 포함된다고 기술할 때 쓰인다. 위에서는 배열의 길이가 [1, 100]이라는 닫힌 집합에 속한다고 명시하고 있다. 경우에 따라서는 \(\mathbb{N}\), \(\mathbb{Z}\) 등을 활용해 원소가 자연수에 속하는지, 정수에 속하는지 등을 표현하기도 한다.
  • 이런 건 다 어디서 주워들어서 쓰고 있다. 필요하면 다 찾아진다.
• 출력: 출력은 최종적으로 어떤 결과를 내야하는지, 그 자료형은 무엇인지에 대해 적는다.
• 처리: 문제의 주요 조건을 적는다. 이때 주요 조건을 놓치지 않도록 조심한다. 짧은 한 문장을 놓쳤을 때 문제가 안 풀리는 경우도 잦다.

여기까지가 체계화 부분이다. 위와 같이 정리해놓으면 다양한 문제를 만나도 일정한 형태가 유지되기 때문에 문제를 풀다가 어떤 조건을 다시 찾아봐야할 때 한눈에 찾기 쉬워진다. 그리고 수학적 표기를 사용하면 짧은 기호로(손 노동으로) 구체적인 정보를 기술할 수 있어 경제적이다.

위의 사진에서 IDEA라고 적어놓은 부분이 ‘핵심 아이디어 추출’과 관련한 부분이다. 다음 세 절에 걸쳐 내가 핵심 아이디어를 추출하고 이를 코딩 전에 정리하는 과정을 살펴보자.

3.1. 알고리즘 선택: 입력의 크기를 바탕으로

문제를 이해했으면 이제 이 문제를 어떤 방법으로 풀어야 할지를 생각해본다. 여기서 방법이란 어떤 알고리즘을 사용할지, 어떤 자료구조로 이 알고리즘을 최대한 효율화할지 등에 대한 생각이다.

이때 어떤 알고리즘을 사용할지에 대한 실마리를 떠올렸다고 해보자. 이 문제를 보고 떠오른 생각은 ‘원 숫자가 될 수 있는 모든 숫자를 만들어서 이 숫자들이 모든 기록을 통과하는지 확인하는지(AND) 검사해보자’이고 이것이 곧 브루트포스(brute force) 또는 완전탐색(exhaustive search)이다. 그러면 입력의 크기 등의 조건을 확인해서 이 알고리즘이 충분히 실현가능할지를 확인한다. 여기서 ‘실현가능할지’는 문제가 풀리는지가 아니라, 입력이 정해진 크기의 상한일 때 적당한 선의 시간이 걸리고 끝날지를 의미한다. 이는 당연한 말이다. 시간이 너무 오래 걸리면 ‘시간 초과’로 탈락하고 마는 모습을 우리는 잘 알고 있다.

완전탐색이 여기서 충분히 실현가능할지 시간복잡도를 대충 계산해보자.

만드는 숫자가 몇 진수인지에 대한 정보가 B, 추측의 크기(records)를 R, 하나의 추측과 원 숫자 후보를 비교하는 비용이 F(n, r)이라고 할 때 완전탐색의 시간복잡도는 $$O(_BP_3RF(n, r)) = O(B^3RF(n, r))$$라고 쓸 수 있겠다. 이 알고리즘은 정말로 실현가능한가?

• 여기서 숫자는 10진수다. 그러면 세 개의 숫자를 고르는 순열의 가짓수, \(_{10}P_3\)은 1000도 안 되는 작은 수다.
• \(R\)은 최대 크기가 100이다. 매우매우 작은 수.
• 마지막 \(F(n, r)\)은 한눈에 들어오지 않는데, R[i] 의 크기가 3밖에 안 되고, 원 숫자의 길이(digit)도 3밖에 안 되는 것을 감안하면 짜기에 따라 조금씩 다르겠지만 결코 크지 않을 것이라 예상된다.

결론은 완전탐색이 가능할 것 같은 복잡도다. 만약 진수 B가 10000진수였다고 해보자. 그 숫자는 16진수처럼 알파벳으로도 다 표현이 안 돼서 아마 한글 글자(‘꿹’, ‘쯟’ 등)까지 사용해야 할 것 같은데(한글 글자의 개수가 11172개다), 이에 대해 숫자 세 개를 뽑는 순열의 가짓수는 1조(\(10^{12}\))를 넘기기 때문에 이 시간복잡도를 갖는 완전탐색은 실현 불가능할 것이다. 그때는 이 알고리즘을 포기하고 더 효율적인 알고리즘을 찾아야 한다. 하지만 입력이 이렇게 작기 때문에 완전탐색이 전혀 문제가 안 되고, 이 경우에는 오히려 ‘완전탐색을 장려하는 문제가 아닌가’라는 의심까지 든다.

여기서 문제 체계화의 중요성이 다시 강조된다. 입출력의 크기 등에 대한 정보를 제대로 파악하지 못했다면 떠오른 방법이 괜찮은지 파악하기 어려웠을 것이다. 아마 감에 의존했거나. 감을 믿지 마라. 인간의 감각정보 처리나 사고는 합리적이기 힘들다. 이 땅에 얼마나 많은 가짜 계시를 받은 구세주들이 존재했는지.

입력의 크기를 바탕으로 완전탐색이 충분히 실현가능하다는 것을 파악했기 때문에 여기서 더 나아가보자.

3.2. 문제 분해 및 조합

‘코끼리를 먹는 방법은 한 입씩 베어 먹는 것이다’라는 유명한 격언이 있다. 코끼리는 너무 크기 때문에 한 번에 삼킬 수 없고 한 입씩 조금씩 먹어서 다 먹자는 뜻이다. 이 뚱딴지 같은 소리는 여러 영역에서 다른 의미로 생각해볼 수도 있겠는데 프로그래밍에서는 다음과 같이 해석해볼 수도 있다.

거대한 원 문제를 있는 그대로 코드로 다루려고 하지 말고, 가급적 단일한 기능을 수행하는 부분문제(subproblem)로 나누어 이 문제들을 해결하고 이들을 조합해 원 문제를 해결하자

이는 꼭 프로그래밍에 국한되지 않고 인생의 많은 분야에 적용할 수 있는 위대한 격언이다. 작게 생각하자. 조금씩조금씩. 그리고 하루를 살아가다 보면 내가 어딘가에는 가있지 않은가.

자, 우리는 완전탐색 알고리즘을 사용하기로 했다. 이 문제는 간단하기 때문에 다음과 같이 크게 두 개의 부분문제로 나눠볼 수 있겠다.

• 모든 가능한 숫자 만들기
  • 우리는 길이가 3이고 각 자리수가 서로 다른 10진수를 만들어야 한다. 이 숫자를 만드는 것도 일이다. 파이썬처럼 조합, 순열 도구를 제공하는 언어를 사용한다면 이를 쓰면 되지만, 아닌 언어를 쓴다면 조금 고민해볼 문제가 된다.
• 특정 숫자와 모든 기록(records)이 일치하는지 검사하기
  • 가령 모든 가능한 숫자를 만드는 도중 ‘123’이 나왔는데 이 숫자가 records 의 모든 원소에 대해 기록된 볼과 스트라이크를 내는지 판단해야 한다.
  • 이때 가급적 단일한 기능이라는 조건 하에 이 부분문제를 한 번 더 쪼갠다:
    • 생성된 숫자와 특정 기록이 일치하는지
    • 이를 AND 조건으로 엮어서 생성된 숫자가 모든 기록에 일치하는지

별로 어렵지 않다. 다만 가급적 단일한 기능에 맞게 잘게 쪼개는 것에 신경쓰자. 원 문제와 직접적으로 연결된 부분문제뿐 아니라 원 문제와 부분문제의 트리도 얼마든지 만들 수 있다.

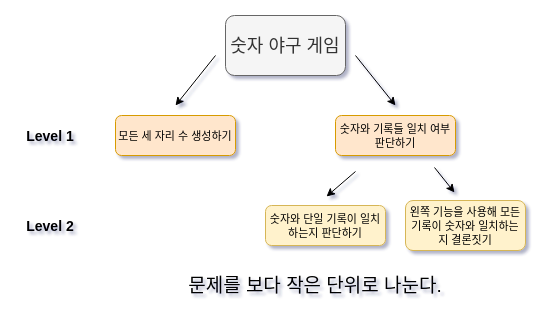
이때 각 Level에 맞는 부분문제의 해답을 조합하면 상위문제가 해결되는 경우가 많다. 이렇게 원 문제에서 부분문제를 나누면 한 번에 코드를 작성하는 것보다 가독성이 증대되고, 따라서 부분 기능에 대한 전문화와 유지보수가 쉬워진다. 특히 원 문제가 어렵고 복잡할수록 이 방법은 장점을 넘어선 필수가 되기도 한다. 어떻게 보면 추상화와도 관련 있는 부분이기도 하다. 이 장점은 실제 코드에서 확인할 수 있을 것이다.

분해 과정을 살펴봤다. 이제 조합 과정을 살펴봐야 하는데 나같은 경우에 조합 과정은 문제마다 다르게 하는 것 같다. 어디서는 사용 가능한 방법이 다른 데서는 사용 가능하지 않은 경우가 있기 때문이다.

이중에서 나는 부분문제를 조합해 원 문제를 해결하는 과정을 수식으로 표현하는 것을 정말 좋아한다. 이 문제의 경우에는 수식으로 표현하는 것이 가능하고, 이 조합 과정이 완성되면 이를 코드로 옮기기만 하면 된다. 다음 절에서 마지막으로 이 부분문제들을 수식적으로 표현해 원문제의 정답으로 만들어보자.

3.3. 조합: 수식으로 정리

나는 야메로 수식 표기법을 배웠다. 일단 종만 형님의 덕이 컸고, 또 내 수학 과외선생 윤 모씨의 도움도 무시못한다. 그리고 필요할 때는 인터넷으로 검색해보기도 한다. 난 이 문제를 수식으로 이렇게 정리해봤다:

\[ \displaylines{ \text{만들 수 있는 모든 세 자리수의 집합을 } N \text{,} \\ \text{모든 추측 기록들의 집합을 } R \text{,} \\ \text{특정 세 자리수를 하나의 추측 기록에 대조해 볼, 스트라이크 개수가 맞는지} \\ \text{판단하는 함수를 } judge(n, r) \text{라고 하자.(n이 숫자, r이 추측 기록)} \\ \text{이때 원 문제의 해답은:} } \]

\[ \large{|{ \forall n \in N | \hspace{2mm} n \hspace{5mm} if \hspace{3mm} \sum_{i=0} \big(judge(n, R[i]) == |R|) }|} \]

저 수식은 양쪽 끝에서 양파 벗기듯 이해하면 쉽다.

• 먼저 맨 바깥의 | |은 안에 있는 집합의 크기를 표현한다고 했다. 종만 형님의 방식이다.
• 그 안의 { }은 집합 표기다. 파이썬에서도 set에 같은 기호를 쓴다.
• 그리고 A가 거꾸로 뒤집힌 \(\forall\) 기호는 집합에서 ‘모든’을 의미한다고 한다. 위의 왼쪽 표현은 ‘N에 속하는 모든 원소 n에 대해서’ 정도의 의미로 썼다. 왼쪽에 쓴 것은 조건을 의미한다.
• 이후 식이 실제 집합의 구성원소를 정의하는데, \(\sum\)을 써서 모든 기록(R[i])과 숫자들을 대조한 결과 참인 값들의 합이 기록 배열의 크기와 같다면, 다시 말해 ‘전부 기록과 일치한다면’ 이 숫자는 내가 추측한 원 숫자일 수도 있다. 저 if 문을 통과하는 세 자리수 n 은 원 숫자의 후보가 될 자격이 있는 것이다.
• 결과 생성된 집합은 원 숫자의 후보가 될 수 있는 모든 숫자들을 원소로 갖는데, | |를 쓰니 그 크기가 반환된다.

와… 이 수식 만들기도 너무 힘들었다. 뭔가 파이썬의 comprehension처럼 식이 만들어졌는데 이는 현재 내가 표현할 수 있는 능력의 최대치다. 분명 수학적 표기법을 제대로 공부한 분들은 더 좋은 표기를 쓸 수도 있겠지. 근데 정말 중요한 건 내가 이해할 수 있는지인데, 일단은 난 이 식이 이해가 간다.

그러면 이런 질문을 할 수 있다. 왜 굳이 수식으로 표현하지? 그냥 일반 문장으로도 얼마든지 부분문제들을 잘 조합하는 문장을 만들 수 있는데? 여기에 내가 할 수 있는 답은 다음과 같다.

• 수학적 표기법은 깔끔하다.
  • 수학적 표기법은 그 의미만 공유되면, 전달되면, 이해할 수 있으면 같은 의미를 전달해도 용량, 즉 길이가 짧다. 그래서 어느 정도 익숙해지면 문장으로 쓰는 것보다 오히려 가독성이 더 좋다.
• 수학적 표기법은 현실의 문장과 달리 오해의 여지가 없다.
  • 가령 A 또는 B라는 현실의 문제는 오해할 수 있다. 이 문장은 수학적으로는 ‘A, B’ 모두 참일 수 있다것을 뜻하는데 그럼 ‘그는 부산 또는 서울에 있다‘가 서울과 부산 모두에 있다는 뜻인가?
  • 현실의 문장은 이와 같은 오해의 여지를 만들어낼 수 있는데, 수학적 표기는 잘 쓰면 그런 가능성을 없앨 수 있다. 수학적 표기를 사용하면 위의 문장도 ‘부산과 서울 모두에 있을 때’와 ‘부산 또는 서울 중 한 곳에만 있을 때’를 구분해서 표현할 수 있다.

물론 이는 내 주관이며, 경험칙으로는 일반적인 코테에서는 수식에 목맬 필요는 없다. 하지만 수식 정리가 매우 강력할 때가 있는데, 점화식을 표현하는 완전탐색 또는 동적 계획법 알고리즘에서는 수식으로 표현하면 이후 과정이 매우매우 수월해진다. 동적 계획법은 점화식을 코드로만 옮기면 되기에 수식 정리가 매우 유용하다.

하지만 수식으로 정리가 힘든 경우도 있다. 개인적으로 이번 2020 카카오 블라인드 테스트 2번 문제가 그랬는데, 이 문제는 수식 정리보다는 그 과정을 잘 스케치하는 게 중요했던 것 같고 수식으로 정리도 못하겠다. 결국에는 상황에 맞게 문제를 정리하고 조합하는 방법을 선택하는 게 정답이겠다.

4. 실제 코드

상술한 내용을 바탕으로 코드를 실제로 작성한다. 나같은 경우에는 Level 1 부분문제들은 함수 안에 클로져 함수로 두고, 최종적으로는 이들을 조합해 답을 내는 것을 선호한다. 코드는 다음과 같다.

def solution(records):
    # 0. 상수, 변수 정의. 숫자 야구는 네 자리수로 하기도 해서 상수로 처리
    MAX_LEN = 3
    ans = 0
    
    # 1. 각 숫자가 한 조건을 통과하는지 살핀다.
    def does_match(n, record):
        b, strike, ball = record
        n, b = str(n), str(b)
        total_strike = sum(na == nb for na, nb in zip(n, b))
        total_ball = len(set(n) & set(b)) - total_strike
        return (total_strike, total_ball) == (strike, ball)
    
    # 2. 숫자를 생성한다.
    def generate_number(tmp_num, used):
        nonlocal ans
        if len(used) == MAX_LEN:
            if all(does_match(tmp_num, record) for record in records):
                ans += 1
            return
        
        for n in range(1, 10):
            if n not in used:
                used.add(n)
                generate_number(tmp_num * 10 +  n, used)
                used.remove(n)


    # 3. 조합해 문제 해결
    generate_number(0, set())
    return ans

말했던 그대로, Level 1 부분문제: ‘모든 세 자리수 만들기’와 ‘생성된 세 자리수와 단일 기록이 일치하는지’는 클로져 함수로 원 solution 함수 안에 둔 것을 확인할 수 있다.

• 순열을 생성하는 것은 python의 itertools.permutations 내장 도구를 써도 충분했는데, 그냥 만들었다. 종만 형님 덕에 난 재귀를 참 좋아하는 사람이 된 것 같다. 구체적인 내용은 이전 포스트에서 다루었기 때문에 넘어간다.
• 숫자와 단일 기록을 비교하는 does_match 함수는 내 방식대로 만들었는데 다르게 만드는 것도 가능해보인다.
  • 두 수의 자릿수를 각각 비교해 strike, ball의 개수를 세고, 그것을 기록된 strike, ball과 비교해 일치하는지 검증한다.
  • 이 함수를 조합해 전체 기록과 숫자가 일치하는지는 중간에 all 함수에서 검증하고 있다. 이 고결한 내장 함수는 모든 조건식 원소에 대해 AND 논리 연산을 한 결과를 반환한다. 최종결과가 True면 이 세 자리수는 어쩌면 원 숫자일 수도 있다.

이렇게 문제를 정의하니 코드 작성은 얼마나 쉬운지. 만약 있는 도구 썼으면 더 짧아졌을 것이다. 멀고 멀리도 왔지만, 이와 같은 과정이 내가 알고리즘 문제에 접근하는 방식이다.

5. 내 방식의 문제점

난 문제를 정리하는 내 방식에 문제가 많다고 생각한다. 다시 말해 개선의 여지가 뚜렷해보인다. 내가 생각하는 문제는:

• 알고리즘 검증이 없다.
  • 종만 형님은 이를 매우 잘 수행하고 계시던데, 난 이 능력이 부족하다.
• 유사코드 등을 사용해서 좀 더 코드에 가깝게 작성할 필요도 있다.
  • 문제가 매우 어려워지면 이런 것도 필요하다. 가령 이진 탐색은 생각보다 온전하게 구현하기 어려운데, 루프 불변식 등을 활용해서 완벽하게 구현하면 좋겠는데 이런 능력이 아직 부족하다.
• 부분문제를 보다 정확하게 묘사할 필요가 있다.
  • 각 부분문제에 대해서도 입출력을 정의한다든지 하는…

인데 아직 어떻게 이를 달성할 수 있을지 모르겠다. 윤 선생한테 다시 과외 받고 싶어지는데, 문제점을 의식하고 있으니 찬찬히 개선해볼 수 있도록 해야겠다.

6. 마치며

와… 생각보다 길어졌다. 힘들었다. 이상이 내가 알고리즘에 접근하는 방법이고, 이는 개선과 수정이 얼마든지 더 가능할 것이다. 보다 좋은 방법이 있으면 주저없이 댓글 달아주시면 좋겠다. 과학자의 올바른 태도는 얼마나 열정과 노력을 들였든 자신의 이론이 틀렸거나, 상위호환의 대안 이론이 출현하고 합리적이면 피눈물을 흘릴지언정 수긍하고 새로운 것을 배우는 것이다. 나는 진심으로 더 좋은 정리 방법을 찾고 싶다.

다시 한 번 말하지만 이 방법은 나만의 정리방법이고 어떤 경우에나, 모두에게나 적절한 방법은 아닐 것이다. 그래도 코드 이전에 문제를 정리하는 것만은 모두가 했으면 좋겠다. 3장의 첫 절의 인덱스가 1이 아닌 0부터 시작하는 것에는 이런 뜻이 있었다. 자신이 이해하기에 좋고, 깔끔한 문제 정리 방법을 고안하는 것. 지금 도전하세요.

다음 포스트는 아마 Knowledge 쪽이 될 것 같다. 최신이 좀 늦었네. 어떤 주제로 해볼까. 벌써부터 고민이 된다.

이상 포스트를 마칩니다.

7. 자료 출처

• bulls and cows: Wikipedia
• 숫자 야구: namu wiki
• 조합과 순열: Parkito’s on the way