![[Python] Get longest palindromes in string](/assets/img//algorithm/longest-palindromes-logo.png)
[Python] Get longest palindromes in string
0. Index
1. Prologue
This is my second post written totally in English. Well, this post was one of my must-do items but I couldn’t make it because I was too lazy. If you’re intested in algorithm, this subject would be attractive, and maybe a piece of cake to you. Today’s post is about palindrome. Palindrome is the very famous, easy-to-introduce algorithm for newbies in computer science or any computer languages. But often, it just focuses on telling whether the given string is a palindrome or not. It’s worth noting but we want more, right? So, today’s post is about ‘getting a list of longest palindromes in a string’. A string can be any sizes long and we have to find all longest palindromes.
I think you wouldn’t know my focus on posts on algorithms because they’re all written in Korean. I try to introduce various solutions on a single problem and to modularize it into several parts. This kind of behavior is really important for other cases and it’s my pride on my algorithm posts.
So, I’ll solve the problem in 2 ways today: One way is really simple, codes are short and I didn’t put my attention too much because problem itself is not that difficult actually. But, the codes are only written in hands and it’s not good. We’ll see what’s and why’s wrong in first solution. And in 2nd solution, we’ll divide it and solve it continously and assemble them. While doing so, we’ll use dynamic programming and improve time complexity of the algorithm. Also, you’ll get to know this way is much more beautiful and healthy for maintenance, reusabilly and for your mental health.
OK, I was too talkative. Let’s move on and dive into algorithm.
2. Problem introduction
Today’s post is about ‘getting a list of longest palindromes in a string’. Palindrome is a sequence of characters which reads the same backward as forward, such as ‘hannah’, ‘racecar’, ‘기러기’. If you’ve studied programming anyhow, I think you might have come across this word or problem related to this. Even if not, it’s okay cause problem is easy and intuitive. We feel comfortable within 2-dimensional areas.
We’re given a string. It can be any string and you have to return a list. Here’s an example.

As you can see, somebody emphasizes importance of levelness of the ground for multi-pulpose radars. His words are given as a string. And we have a function named ‘get_longest_palindromes’ and this function returns longest palindromes. This sentence has two longest palindromes and they’re ‘level’ and ‘radar’. They’re both 5 chars long. So the returned list has two items inside.
And if a string has no palindromes(like ‘abc’), it returns a list of all characters([‘a’, ‘b’, ‘c’]) cause a character of one length is a palindrome technically. If an empty string(‘’) is given, we return a list of an empty string(['']).
3. Way 1: Implement it simple way
Palindrome is an easy example of many brain-*ucking problems related to string and we can solve it without any sort of deep thinking or taking notes. With definition, we can know that length of longest palindromes is between 0(inclusive) and length of the original string(inclusive). If so, how about iterating N to 0(not 0 to N) and test all substrings in a string if they’re palindromes. If any substring matches, we can iterate until that candidate length and finish the loop cause we don’t need short palindromes in this problem.
I just created the simple version of ‘get_longest_palindromes’ function. It’s only 2 for loop deep and codes are short too.
def get_longest_palindromes(strng):
N = len(strng)
ans = []
for l in range(N, 0, -1): # 1.
found = False
for s in range(N-l+1): # 2.
target = strng[s:s+l]
if target == target[::-1]: # 3.
ans.append(strng[s:s+l])
found = True
if found:
break
return ans if strng else [''] # 4.
Here’re some comments on codes section 1, 2, 3 and 4.
- We first iterate on possible longest length in [N, 1]
- We don’t need to check 0 because shortest palindromes are one length long if not string is empty.
- And we define found variable to check if we found palindromes in that candidate length. At every end of first loop, we’ll check if found is changed and end the loop if longest palindromes are found and saved.
- Check every substring of length l if it is a palindrome
- Look at the length of iteration of 2nd loop. It’s \(N-l+1\), not \(N-l\). It may seem confusing but simple. If \(l == N\), we have to iterate only once. But if we don’t add 1 in iteration count, no iteration is executed.(N-N is 0 and range(0) is not executed) So we have to add 1. To be honest, I was really confused at first.
- Direct codes of checking a substring is a palindrome
- With length variable(l) and start location of a substring(s), we can retrieve a target substring. And now what’s left is checking it. There can be a lot of ways to check but we use a very easy and intuitive way. Just compare the substring to backwards string. We used a Python trick to reverse a Sequence backwards. Using -1 stride
- If we found palindromes, we append to the ans list and toggle found variable to True.
- After all iterations, we return the ans. But We didn’t consider a case of an empty string. If so, return [''] or return ans otherwise.
How do you think of this codes? Well, I can solve it in this way but I won’t recommend this kind of algorithms and approach for the original problem. I train myself to maintain a negative view on this kind of approach actually. This codes don’t imply any philosophy.
Next algorithm is way more appropriate for this purpose. It needs more time and energy, insight on the question but I assure you that you will be more satisfied with algorithm.
4. Way 2: A more elegant way
We checked out an easy solution for the question. Yes, it perfectly works but I don’t like this way. We can be more than what this way insists.
In this chapter, I’ll first explain what’s wrong and missing in the previous solution. And next we’ll cover two improvement proposals: modularizing the problem and using dynamic programming for time complexity.
4.1. Easy one first: define subproblem
How do you feel about the previous solution above? I just ran into the codes and it just took 5 minutes to weave the code blocks to solve the problem. This problem was not that difficult so this way of working worked well. But if a problem gets slighly more harder and complicated, we won’t be able to make it.
Before solving it, we have to think first and take notes of the problem. And if we can, we have to divide the original problem into easier subproblems so that we can assemble it and solve the original. Like we play Legos: using many type of blocks and making a full machine.
This way of thinking and dividing the problem would seem tiresome at first. But if the problem keeps getting complicated, we cannot handle it, cause it’s too big and not structured. You cannot progrm Microsoft Excel in a single function. So think first, define subproblems and lego them into a system.
The original problem is ‘Get list of longest palindromes in a string’. And I divided it into subproblems:
- A function that tells if a given string is a palindrome or not.
- How to get the length of longest palindromes in a string.
- Get all longest palindrome substrings and return it into a list.
Each subproblem is much easier than the original, complicated and mixed problems. And let’s solve it one by one. Then we would feel no hardship when encountered a harder one.
4.2. Need for a more efficient program
OK, we defined some subproblems. And what’s next? Problem is much easier than before and we can consider efficiency that we wouldn’t be able to imagine when the problem is too complicated.
Here are the very core part of the previous solution.
...
for l in range(N, 0, -1): # 1.
found = False
for s in range(N-l+1): # 2.
target = strng[s:s+l]
if target == target[::-1]: # 3.
ans.append(strng[s:s+l])
found = True
if found:
break
...
How would time complexity of the solution be? There are 2 for loops nested and checking if a string is palindrome(sec. 3) is \(O(n)\). So the total time complexity is \(O(N^3)\). There’re some cases that possible best solutions works \(O(N^3)\) but normally, this time complexity is not good. It takes \(10^9\) calculations even if the input is only 1000. It would take several seconds at least.
With the power of modularity, redefining the problem into subproblems, we can specialize each part and replace inefficient parts with new, better codes. Now, I think I can improve the subproblem No.1 among three of them in the previous solution. It’s about checking a substring.
4.3. Tuning the subproblem: How to tell a palindrome
Our code for checking a substring is a palindrome or not is like this:
for l in range(N, 0, -1): # 1.
found = False
for s in range(N-l+1): # 2.
target = strng[s:s+l]
if target == target[::-1]: # 3.
ans.append(strng[s:s+l])
Getting a substring and reversing it is really easy in Python. But at worst cases, we have to check all substrings and this won’t make it.(\(O(N^3)\))
So, let’s define a subfunction is_palindrome. It gets lo, and hi variables, which are the start and end indices of a target substring.(both are inclusive)
\[ \text{is_palindrome}(lo, hi): \text{Return bool value of whether a substring(string[lo, hi]) is a palindrome or not} \]
With this definition, we can induce a recurrence formula:
\[ is\_palindrome(lo, hi) = \displaylines{ \begin{cases} True & \quad \text{1. if lo == hi}, \\ string[lo] == string[hi] & \quad \text{2. if lo + 1 == hi}, \\ False & \text{3. if string[lo] != string[hi]}, \\ \text{is_palindrome}(lo+1, hi-1) & \quad \text{4. else} \end{cases} } \]
What does this mean? True or not is decided by one case among this conditions.
- If lo is same to hi, it means a single substring and the answer is always True.
- If lo+1 is same to hi, it means substring is two chars long and the answer is whether each character is same or not.
- Otherwise, it’s divided into 2 cases:
- If two outermost characters in a substring are different, it cannot be a palindrome and return False.
- Else, we have to check for a smaller substring[lo+1, hi-1].
Understanding case 3. is important. Let’s assume our target substring is ‘ABCBA’. How can we know if it’s a palindrome?
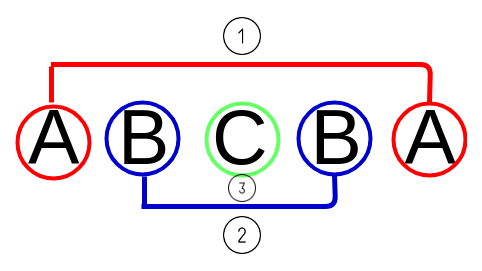
Palindrome is like an onion. When you strip off outermost characters, the left substring is also a palindrome. Outermost characters here are ‘A’, ‘B’ and ‘C’ in sequence. And both edge characters should always match each other in palindrome, and it’s not if they don’t.
So when we finish the first comparing process, comparing outermost chars, we can go to next outermost chars until we reach the base cases defined above: case No 1, 2.
If outermost characters match(if string[lo] == string[hi]), we can call recursive function in the range of [lo+1, hi-1](process No.2).
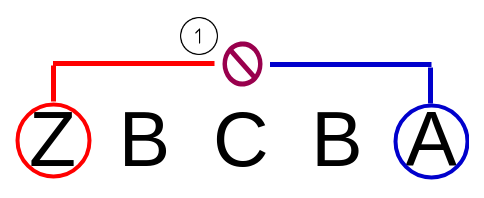
However, what about if outermost characters are different? Then, string cannot be a palindrome at all. No need to check inner characters. Then return False.
OK. Understood. What can we do now? With recursive function, we can know that if we already know the answer of smaller problems(like [lo+1, hi-1]), it’s easy to know the answer of bigger problem([lo, hi]). And we have to store the state(answer) of smaller problems and it’s perfect time to use cache.. Dynamic programming is a perfect match here.
4.4. Let’s dive into Code
We concluded it’s better to use dynamic programming and let’s implement it in this way.
First, we can create the cache
def get_longest_palindromes(strng): # 1.
N = len(strng)
cache = [[None] * N for _ in range(N)] # 2.
- We defined get_longest_palindromes function and it takes ‘strng’ variable.
- Defined a cache. Our is_palindrome subfunction takes two elements lo, hi. So we need to track the states related to them. That’s why cache is a 2D matrix.
With cache, we can implement get_longest_palindromes function using it.
def is_palindrome(lo, hi):
if cache[lo][hi] is not None: # 0.
return cache[lo][hi]
if lo == hi: # 1.
return True
elif lo + 1 == hi: # 2.
return strng[lo] == strng[hi]
# 3.
ans = False if strng[lo] != strng[hi] else is_palindrome(lo+1, hi-1)
cache[lo][hi] = ans
return ans
Our cache is initialized with None at first. And if we find answer of a problem, we can record it. If it’s not None, we solved this problem before, so no need to repeat it. Just return the answer.
And section 1, 2 and 3 are just Python implementation of our recurrence formula. Literally same. If we can induce a recurrence formula, things go easy with coding many times.
If we get answer of range in [lo, hi], we record it in the cache and return it.
Jule! We finished our first subproblem.
The rest subproblems are:
- How to get the length of longest palindromes in a string.
- Get all longest palindrome substrings and return it into a list.
But these problemsa are pretty much similar to the codes of first solution. Here are codes solving these 2 subproblmes.
def generate_palindromes():
ret = []
longest = N
found = False
if not strng:
return ['']
for l in range(N, 0, -1):
found = False
for s in range(N-l+1):
if is_palindrome(s, s+l-1):
found = True
ret.append(strng[s:s+l])
if found:
break
return ret
I created generate_palindromes subfunction getting the longest palindromes using our is_palindrome subfunction.
And we start longest length from N, as we did above. And I set found variable to False and this will be toggled on if we found longest palindromes. Then no more loop iteration is needed. After end of 2nd iteration, we check everytime if found is toggled on and breaks out if it’s True
It’s noteworthy that I combined two subproblems into a single subfunction. If a subproblem is too easy, no need to make it a single module. You can assemble it into a bigger one. In my rule of thumb, when you’re not sure if you have to define a single function or not, it’s better to make it a function and independent. Because it’s easier for maintenance.
OK. All modules are ready. We can combine them into a function solving the original problem.
def get_longest_palindromes(strng):
N = len(strng)
cache = [[None] * N for _ in range(N)]
def is_palindrome(lo, hi):
if cache[lo][hi] is not None:
return cache[lo][hi]
if lo == hi:
return True
elif lo + 1 == hi:
return strng[lo] == strng[hi]
ans = False if strng[lo] != strng[hi] else is_palindrome(lo+1, hi-1)
cache[lo][hi] = ans
return ans
def generate_palindromes():
ret = []
longest = N
found = False
if not strng:
return ['']
for l in range(N, 0, -1):
found = False
for s in range(N-l+1):
if is_palindrome(s, s+l-1):
found = True
ret.append(strng[s:s+l])
if found:
break
return ret
return generate_palindromes()
print(get_longest_palindromes('hannah'))
print(get_longest_palindromes('racecar'))
print(get_longest_palindromes('foobarisreadytogo'))
print(get_longest_palindromes('abcdef'))
print(get_longest_palindromes(''))
['hannah']
['racecar']
['ogo']
['a', 'b', 'c', 'd', 'e', 'f']
['']
I admit that codes are much longer than before. However, our purpose is not making a short program but a more beaufitul and efficient program. What benefits have this solution gained?
- Readability: With defining subproblems and making them modules, readability improved. And that’s why we define problems and modularize blocks.
- Efficiency: As readability is improved, we can talk about better efficiency. Amongst subfunctions, bottleneck part is ‘checking a string is a palindrome’. We can profile a program better and we changed is_palindrome function in design level. And if we find a better solution than dynamic programming, no need to make a mess. Just improve the codes of a subfunction. Much, much more easy.
By the way, what is time complexity of this solution? We know that ‘checking a palindrome’ was a bottleneck. And time complexity of is_palindrome function is \(O(N^2)\) cause cache size is \((N^2)\). So the total time complexity is \(O(N^2)\), much better than \(O(N^3)\), complexity of the previous one.
OK, we made a better solution with power of defining subproblems, modularity and assembly of them into a final solution.
5. Appendix: importance of defining problems
When I first solved the problem, my solution didn’t use ‘checking a palindrome’ part. In our functions, we define is_palindrome function and its specification is like this:
[\begin{align} \label{} \text{is_palindrome}(lo, hi): \text{Return bool value of whether a substring(string[lo, hi]) is a palindrome or not} \end{align}]
This is how we defined a subproblem. But I didn’t mention it’s the only or best to way solve the problem. My first solution defined the other function to use dynamic programming:
[\begin{align} \label{} \text{length_of_longest}(lo, hi): \text{Return length of longest palindrome in a substring(string[lo, hi])} \end{align}]
While our code stored True or False if the substring in range [lo, hi] is a palindrome or not, my original function stored length of longest palindromes in range [lo, hi]. So if substring were ‘abac’, stored value would be ‘3’, not ‘False’.
And with this subfunction, you can also solve the problem too, but it gets much more messy.
I recommend you to solve the same problem with this subfunction. I got to know importance of defining (sub)problems. Whole codes and solution is totally changed for the same problem and I even used dynamic programming there too. It’s really interesting and implies a lot. Remember, define the problems first. It directs where you should go, and controls whole logic.
6. Epilogue
We looked through the ways to solve ‘Get longest palindromes in a given string’. First was simple but not considered enough. Solution was made of just one block so handling it was not easy. But the second one was much better. It took more time and codes to define subproblems and assemble them, but much better in the sense of efficiency, readability and maintenance.
To be honest, I feel less confident on this post. I’m not sure if my first purpose is accomplished for readers: Emphasizing importance of modularity and deep thinking before diving into coding. English words are confusing and I feel strange to type in English now. I cannot say my semi-major was English Literature and I’m shameful :P. I hope you guys understand flaws in my English.
But I feel relieved that I just ended the post of one of my candidate subjects piled up in my head.
What would be the next topic? Anything would be good if it interests me and you. :)
Post ended.
