
1차원 배열 회전 알고리즘 5가지
목차
- 들어가며
- 배열을 회전한다는 것은?
- 알고리즘 살펴보기
- 3.1. Python 배열 슬라이싱
- 3.2. 배열 값 이동
- 3.3. 반전에 반전(Reverse the reversed)
- 3.4. 저글링(Juggling)
- 3.5. 분할정복
- 마치며
1. 들어가며
결국 작업에 착수하게 됐다. 어느 포스트엔가 배열 회전 알고리즘을 다루겠다고 했는데 쉽지 않은 작업일 것 같아 미루고 미루게 되었다. 하지만 마음속 숙제로 계속 남겨놓기가 그래서 조금씩이라도 해보겠다. 여기 알고리즘들은 기상천외하고 즐거운 것들이 많으니 잘 살펴보도록 하자. 특히 분할정복, ‘Reverse the reversed’가 특히 재밌으니 이 둘은 꼭 살펴보기를 바란다.
여기 알고리즘의 뒤 3가지의 아이디어는『생각하는 프로그래밍』(존 벤틀리 저, 인사이트 출판사)의 칼럼 2를 많이 참고했다.
2. 배열을 회전한다는 것은?
배열을 회전한다는 것은 무슨 의미인가? 어렵지 않다. 먼저 여기서 배열은 1차원 배열을 가리킨다. 그리고 이 배열을 회전한다는 것은 오른쪽이든 왼쪽이든 특정 방향으로 원소들을 이동하는 것을 말한다. 그림이 더 이해가 빠르겠다.
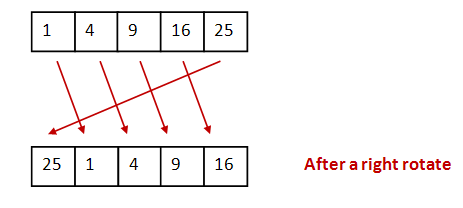
위 그림은 윗 배열을 오른쪽으로 한 번 회전한 후의 모습을 나타내고 있다. 원소들이 하나씩 오른쪽으로 밀린 것을 확인할 수 있는데 이때 맨 마지막 원소인 25는 0 인덱스로 위치를 바꿨다.
우리는 이 배열을 회전하는 알고리즘을 만들자. 배열은 왼쪽, 오른쪽 모두로 회전할 수 있지만 이 포스트에서는 오른쪽으로 회전한다고 가정하고 만들자. 왼쪽 회전도 같이 구현해 기능성을 높이려면 알고리즘마다 작업해줘야 하기 때문이다. 이는 소개할 알고리즘의 핵심은 아니다. 그리고 꼭 한 번만 회전할 필요는 없다. 1번이고, 2번이고, 1000번이고 회전시킬 수 있다. 회전 횟수는 인자로 제어하도록 하자.
이번 포스트 통틀어 사용할 샘플은 arr 배열로 ‘[1, 2, 3, 4, 5]’와 같다고 하자.
이를 오른쪽으로 2번 회전하면 결과는 다음과 같을 것이다.
\[ rotate(arr, 2) = [4, 5, 1, 2, 3] \]
이 결과를 만드는 여러 알고리즘을 살펴보자는 것.
3. 알고리즘 살펴보기
살펴볼 알고리즘은 모두 5가지이다. 초반이 쉽고 뒤로 갈수록 사고가 필요해진다. 특히 마지막 분할정복 방법이 기가 막히는데 살펴보길 바란다.
3.1. Python 배열 슬라이싱
파이썬은 배열이 기본적으로 슬라이싱 인덱스를 지원한다. 슬라이싱은 원 배열에서 0개 이상의 원소를 갖는 부분 배열을 추출해내는 것을 말하며 가령 arr 의 1번째부터 3번째 원소까지를 슬라이싱 하려면 다음과 같이 입력하면 된다.
>>> arr = [1, 2, 3, 4, 5]
>>> print(arr[1:4])
[2, 3, 4]
슬라이싱의 기본 문법이다. ‘[ ]’ 안에 ‘:’를 두고 양옆에 슬라이싱할 시작과 끝 인덱스를 적는데 끝 인덱스는 1만큼 키워서 한다. 파이썬 사용자라면 누구나 알 너무나 기본적인 개념이다. 배열 회전을 구현하는 첫 알고리즘은 이처럼 배열의 슬라이싱을 사용하는 것이다.
아까의 예제를 보자.
‘[1, 2, 3, 4, 5]’ 배열을 오른쪽으로 2번 회전하자 결과가 ‘[4, 5, 1, 2, 3]’으로 변했다. 이때 원 배열의 ‘1, 2, 3’을 ‘L’, ‘4, 5’를 ‘R’이라고 하면 회전 결과는 단순히 R과 L을 순서를 바꿔서 합친 결과와 같다.
\[ \displaylines{ arr = (1, 2, 3) + (4, 5) = LR = [1, 2, 3, 4, 5] \\ rotate(arr, 2) = (4, 5) + (1, 2, 3) = RL = [4, 5, 1, 2, 3] } \]
그러면 회전 알고리즘은 단순히 L과 R을 나눈 뒤 이를 순서를 바꿔 합치면 된다.
def rotate(arr, n):
# 1.
if not arr:
return arr
n %= len(arr)
if not n:
return arr
# 2.
left = arr[:-n]
right = arr[-n:]
# 3.
return right + left
>>> rotate([1, 2, 3, 4, 5], 2)
[4, 5, 1, 2, 3]
정상적으로 작동한다. 매우 간단한데 그 내용을 살펴보면
- 회전 횟수를 배열의 길이로 나머지 연산을 한다.
- 이는 나머지 회전 알고리즘에도 사용하면 좋은데 회전 횟수가 커지면 이를 다 수행할 이유가 없다. 예제에서 배열의 길이는 5인데 이러면 2, 7, 12, 17, …, 5n + 2 번 회전한 결과는 모두 같기 때문. 배열의 크기 이상으로는 회전할 이유가 없다.
- 또 빈 배열이 입력되었으면 모듈로 연산식에서 에러가 발생한다. 그것을 방지하기 위해 빈 값을 체크한다.
- 슬라이싱으로 left, right를 나눈다.
- 나누는 기준은 회전 횟수가 된다.
- right와 left를 뒤집어 붙여 반환한다.
- 파이썬에서는 리스트끼리의 ‘+’ 연산을 허락하며 이때 두 리스트를 접합(extend)한 새 배열이 반환된다. 그래서 위와 같이만 하면 순서를 뒤집어 붙일 수 있다.
슬라이싱 방법의 장점은 코드가 매우 간결하다는 것이다. 줄일 대로 줄이면 10줄도 안 된다. 그럼에도 잘 작동하는 것을 확인할 수 있다.
3.2. 배열 값 이동
두 번째 방법 또한 상당히 직관적이다. 새 배열을 만들어 원 배열의 i 번째 인덱스의 값을 새 배열의 i+n 인덱스에 집어넣는다. 이때 i+n 이 배열의 길이를 넘길 수 있기 때문에 배열의 길이만큼 나머지 연산을 한다.
바로 코드를 보자.
def rotate(arr, n):
if not arr:
return arr
N = len(arr)
n %= N
if not n:
return arr
new_arr = [None for _ in range(N)]
for i in range(N):
new_arr[(i+n) % N] = arr[i]
return new_arr
>>> rotate([1, 2, 3, 4, 5], 2)
[4, 5, 1, 2, 3]
마찬가지로 잘 작동한다. 이번 알고리즘은 for 문만 잘 파악하면 된다. i+n 이 배열의 크기를 넘길 때 나머지 연산을 하면 다시 배열의 앞으로 온다.
3.3. 반전에 반전(Reverse the reversed)
이 알고리즘도 신박하다. 먼저 용어를 정의하자. 어떤 배열에 있어서 배열을 좌우로 완전히 뒤집는 것을 ‘r’(reverse) 연산이라고 하자. 이 ‘r’ 연산자는 배열의 우측 상단에 제곱승수처럼 써넣는다.
\[ \displaylines{ A = [1, 3, 5, 7, 9] \\ A^r = [9, 7, 5, 3, 1] } \]
전혀 어렵지 않다. 회전 알고리즘을 첫 번째 알고리즘처럼 L과 R을 나눠 이를 뒤집는 것이라고 생각하자.
그러면 ‘arr = LR’이라고 쓸 수도 있다. 이때 최종적인 결과는 ‘RL’을 만드는 것이다. 이에 대한 이해와 배열을 뒤집는 ‘r’ 연산을 활용하면 rotate 를 다음과 같이 구할 수 있다.
\[ \displaylines{ arr = LR \\ rotate(arr) = (L^rR^r)^r = RL } \]
우왓 이게 무슨 말인가. L과 R 각각을 뒤집은 뒤, 이것들을 합친 결과 전체를 다시 한 번 뒤집으면 우리가 원하는 RL이 나온다는 것이다. 이 알고리즘의 이름을 내 마음대로 ‘Reverse the reversed’라고 한 것은 다 이유가 있다. 그러면 실제로 그럴까? 간단히 확인해보자.
\[ \displaylines{ arr = [1, 2, 3, 4, 5] \\ L = [1, 2, 3] \\ R = [4, 5] \\ \\ L^r = [3, 2, 1] \\ R^r = [5,4] \\ \\ L^{r}R^{r} = [3, 2, 1, 5, 4] \\ (L^{r}R^{r})^r = [4, 5, 1, 2, 3] } \]
진짜 나온다. 이제 이를 코드로 구현해보자.
# 1.
def reverse(arr):
new_arr = []
n = len(arr)
for i in range(n):
new_arr.append(arr[n-1-i])
return new_arr
def rotate(arr, n):
if not arr:
return arr
N = len(arr)
n %= N
if not n:
return arr
right, left = [], []
# 2.
for i in range(N-n):
left.append(arr[i])
for i in range(N-n, N):
right.append(arr[i])
left_rev = reverse(left)
right_rev = reverse(right)
# 3.
return reverse(left_rev + right_rev)
>>> rotate([1, 2, 3, 4, 5], 2)
[4, 5, 1, 2, 3]
- 배열을 뒤집는 reverse 함수를 만든다.
- 파이썬에는 배열 등을 뒤집는 reversed 라는 내장함수가 존재하기는 하는데, 결과가 바로 리스트가 아닌 이터레이터가 나온다. 그래서 우리가 원하는 바를 달성하려면 추가적으로 list 함수로 감싸야 하는데 그런 중첩을 개인적으로 좋아하지 않아서 그냥 함수를 만들었다. 코드는 상식적인 코드다.
- 원 배열을 좌우 부분으로 나눈다.
- 슬라이싱을 사용하지 않았다. 어려울 것은 없지만 왼쪽을 만드는 for 의 범위가 ‘N-n’이고, 오른쪽을 만드는 범위가 ‘N-n, N’인 것만 확인하면 된다.
- 반전된 좌우를 합친 반전 배열 전체를 다시 한 번 반전해서 원하는 결과를 만든다.
- 이는 앞서 확인한 알고리즘을 그대로 구현했다. 그렇기 때문에 값은 옳게 나온다.
이 알고리즘은 슬라이싱을 사용하지 않았다. 개인적으로 알고리즘 문제를 풀 때는 슬라이싱을 사용하지 않는다. 그 이유는 몇 가지가 있다. 슬라이싱은 배열의 특정범위를 뽑을 때 매우 편하지만 알고리즘 문제를 풀 때는 보다 원시적으로 해서 인덱스와 관련된 시행착오를 겪는 게 맞다고 생각한다. 회사를 들어가면 파이썬 이외의 언어를 써야할지도 모르는데 이때 해당 언어가 배열의 슬라이싱을 지원 안 할 수도 있기 때문이다. 슬라이싱에만 익숙해지면 그때 별 것도 아닌 배열 인덱스 때문에 불필요한 스트레스를 받을 수도 있다.
물론 내 말이 곧 정답은 아니다. 다만 언제나 다양한 해결방법을 아는 것은 나중에 큰 도움이 되기에 같이 소개했다.
3.4. 저글링(Juggling)
가장 무난한 두 번째 방법을 되돌아보자. 그 알고리즘은 원 배열의 크기만큼의 새 배열을 만들어 그 배열에 값을 옮겨 담는다. 이때 필연적으로 새 배열의 크기 N만큼의 공간이 필요해진다. 만약 배열의 크기가 크고 주어진 메모리가 넉넉지 않다면(가령 임베디드 시스템이라든가…) 이 N만큼의 공간도 부담이 될 수 있다.
이때 저글링 방법은 필요한 공간을 1로 줄일 수 있다.
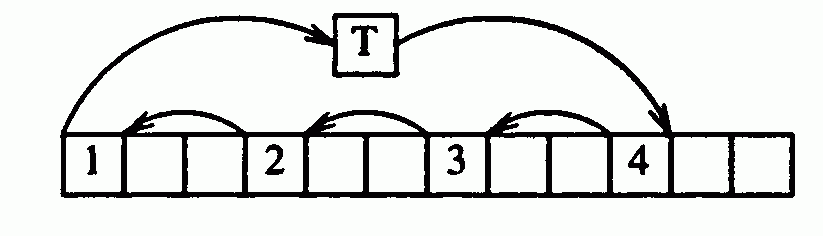
위 그림은 크기가 12인 배열에서 3만큼 왼쪽으로 회전하는 경우를 보여주고 있다. 우리는 오른쪽으로 회전하고 있지만 핵심적인 아이디어에는 전혀 상관없다.
배열을 arr 이라고 할 때 arr[0] 을 T 라는 변수에 저장한다. 그리고 인덱스를 0에서 회전 횟수 n(여기서는 3) 만큼씩 키워가면서, 3번째는 0번째로, 6번째는 3번째로, 9번째는 6번째로 값을 옮긴다. 9에 3을 더한 12는 배열의 마지막 인덱스 11을 초과하기 때문에 멈춘 후 9번째 인덱스에 아까 저장한 T 값을 옮긴다. 그러면 한 사이클이 끝났다.
그리고 다음 사이클을 진행한다. arr[1] 부터 시작하는데 1에서 4, 7, 10까지 진행하면 된다. 사이클은 총 n 번만큼 진행하게 되며 사이클을 모두 마치면 최종적으로 n 만큼 왼쪽으로 회전하게 된다.
오른쪽으로 회전할 때는 값을 옮기는 방향을 반대로 하기만 하면 된다.
근데 이 사이클을 n 번 반복하는 방법은 배열의 길이가 n 의 배수일 때만 쓸 수 있다. 위 경우는 배열의 길이는 12이고, n 은 3이다. 그런데 우리의 예제, 길이가 5고 n 은 2인 경우에는 위와 같이 해보면 답이 틀림을 알게 된다.(그래서 내가 많이 헤맸다.) 따라서 두 경우를 구분해줘야 한다.
배열의 길이가 회전 횟수의 배수가 아닌 경우에는 한 사이클 내에 전부 처리할 수 있다. 배수일 때는 한 사이클이 모든 원소를 바꾸지 못하고 계속 반복 회전하는 데 비해 배수가 아니면 필연적으로 모든 원소를 회전시키기 때문이다. 길이가 5일 때 2씩 옮겨봐라. 한 사이클에 모두 옮길 수 있음을 알게 된다. 이를 구분해서 코드를 만들면 다음과 같다.
def rotate(arr, n):
# 1. Base case 검사
if not arr:
return arr
N = len(arr)
n %= N
if n == 0:
return arr
# 2. 길이가 회전 횟수의 배수일 때
elif N % n == 0:
for last in range(n):
start = N - n + last
T = arr[start]
s = start
while s - n >= 0:
arr[s] = arr[s-n]
s -= n
arr[last] = T
# 3. 아닐 때
else:
s = 0
T = arr[s]
for _ in range(N-1):
arr[s] = arr[(s-n) % N]
s = (s-n) % N
arr[s] = T
return arr
>>> rotate([1, 2, 3, 4, 5, 6, 7, 8, 9], 3)
>>> rotate([1, 2, 3, 4, 5], 2)
- 기저사례 검사
- 배열이 비었거나, 길이로 모듈로한 회전횟수가 0이면 그대로 반환한다. 연산할 이유가 없다.
- 배열의 길이가 회전 횟수의 배수일 때
- n 번의 사이클이 생기기 때문에 그만큼 반복문을 돌린다. 이때 위 그림의 예제에서는 last 가 차례로 0, 1, 2가 되는데, 이 원소들을 last 라고 이름 지은 이유는 사이클의 마지막 원소를 T 로 저장하고 앞의 원소들을 차례로 앞으로 옮기면 마지막으로 last 원소에 아까 저장한 T 를 집어넣기 때문이다.
- start 는 사이클의 마지막이 된다. 위 그림에서는 사이클의 인덱스가 각각 9, 10, 11이 된다. start 를 구하는 식을 눈여겨보자. 실제로 확인해보라.
- while 문을 돌며 앞의 원소를 오른쪽으로 옮긴다. 마지막으로 last 에 T 를 옮긴다.
- 배수가 아닐 때
- 첫 원소의 인덱스를 0으로 잡은 뒤, 그때부터 n 씩 왼쪽 원소를 오른쪽으로 옮긴다. 이때 길이 N 만큼 모듈로를 쓰는 것을 잊지 않는다.
- for 문의 횟수가 왜 N-1 일까? 배열의 모든 원소를 바꿔야 하기 때문에 기본적으로 N 이 필요한데, 그중 한 번은 아까 저장한 T 를 갖다 쓸 것이기 때문에 반복문 이외의 할당식이 필요하다. 그래서 1을 빼준다.
- 마지막 원소에 T 를 갖다 붙인다.
확인해보면 배열의 길이가 회전 횟수의 배수일 때와 아닐 때 모두 잘 작동함을 알 수 있다.
참고로 저글링이란 단어는 곡예사들이 공을 두 손으로 몇 개씩 돌리는 모습이 여기서 원소를 왔다갔다 하는 모습이랑 비슷해보여서 붙인 것 같다. 내가 만든 알고리즘 이름이 아니고 책에서 알려준 이름이다.
3.5. 분할정복
이 방법이 내가 소개하는 알고리즘 중 가장 우아하다. 벡터를 회전하는 데 분할정복까지 쓸 수 있으리라고는 생각조차 못했는데 개발자들은 역시 재미있는 인간들이다.
이 알고리즘은 개념 자체는 그러려니 할 수 있다. 그런데 코드 자체를 구현하는 것은 애를 먹을 수도 있는데 분할정복 식에서 배열 인덱스를 처리하는 것이 조금 까다롭다. 일단 알고리즘의 아이디어를 살펴보자.
먼저 우리에게 배열에서 크기가 같은 두 부분 구간의 값을 교체하는 함수 swap 이 있다고 하자. 이는 C언어에서 두 변수의 값을 바꾸기 위해 자주 만드는 swap 과 같은데 여기서는 교체 대상이 배열의 구간이라는 것이 차이이다. 가령 어떤 배열의 0:3 구간과 7:10 구간은 크기가 같기 때문에 이 둘의 값을 교환할 수 있는데 함수의 인터페이스는 대략 다음과 같을 것이다.
\[ \displaylines{ arr = [1, 2, 3, 4, 5] \\ swap(arr, 0, 3, 2)\\ arr \text{는 다음과 같이 변한다. -> } [4, 5, 3, 1, 2] \\ \\ \text{0과 3 인덱스에서 시작하는 2개씩의 값을 교체했다.} } \]
이 함수를 바탕으로 분할정복 알고리즘을 만들 것이다.
아까처럼 배열 arr 을 n 번만큼 회전하는 것은 앞 부분 A를 앞에서 N-n개, 뒷 부분 B를 n개 선택한 뒤 이 둘의 위치를 바꾸는 것이라고 하자.
\[ arr = [1, 2, 3, 4, 5] = AB = (1,2,3)(4,5) \]
이때 A가 B보다 크기가 큰데 A를 다시 나누자. 이때 앞 부분을 B의 크기와 같게 한다.
\[ \displaylines{ arr = [1, 2, 3, 4, 5] = A^{l}A^{r}B = (1,2)(3)(4,5) \\ \text{이때 우리가 원하는 최종적인 결과는} \\ rotate(arr) = BA^{l}A^{r} = (4,5)(1,2)(3) } \]
arr 은 세 부분으로 나뉘는데 \(A^l\)과 \(B\)의 크기가 같다. 그래서 두 부분 배열을 swap 한다.
\[
\displaylines{
swap(arr, 0, 3, 2) = BA^{r}A^{l}= (4,5)(3)(1,2) \\ \\ 0\text{은} A^{l}\text{의 시작 인덱스,} \\ 3\text{은 } B\text{의 시작 인덱스,} \\ 2\text{는 교체할 구간의 크기}
}
\]
swap 을 한 번 한 결과 우리가 최종적으로 원하는 회전 결과의 B는 제 자리에 왔다. 하지만 A는 오른쪽, 왼쪽 파트가 아직 뒤바껴 있는 상태다. 그러면 A를 대상으로 우리가 한 것을 똑같이 한다.
\[ \displaylines{ \text{B는 해결됐으므로 } A^r, A^l \text{만 회전하면 된다.} \\ 즉, rotate(A^{r}A^{l}) } \]
\(A^r\)의 길이는 1, \(A^l\)의 길이는 2이므로 다시 \(A^l\)을 둘로 나눈다. 둘로 나뉜 결과가 \(A^{ll}\), \(A^{lr}\)이라고 하자. \(A^r\)과 \(A^{lr}\)의 크기가 같으므로 이들을 다시 swap 한다.
\[ \displaylines{ swap(arr, 2, 4, 1) = swap(BA^{r}A^{ll}A^{lr}) = swap((4,5)(3)(1)(2)) \\ \\ arr -> BA^{lr}A^{ll}A^{r} = [4, 5, 2, 1, 3] } \]
마지막으로 \(A^{lr}과 A^{ll}\)만 swap 해주면 끝난다.
여기서 분할정복의 여지를 보았는가? 더 이상 swap 할 필요가 없을 때까지 계속 함수를 재실행하면 우리가 원하는 결과가 나올 것 같다.
먼저 swap 함수부터 만들어보자.
def swap(arr, h, t, size):
# 1.
if h > t:
swap(arr, t, h, size)
# 2.
if h + size > t:
raise IndexError("Swap range is dupliacated")
tmp = [None for _ in range(size)]
for i in range(size):
tmp[i] = arr[h+i]
arr[h+i] = arr[t+i]
arr[t+i] = tmp[i]
return
배열의 두 부분 구간의 값을 교체하는 함수를 만들었다. 실제 동작 코드는 별거 아닌데 기저사례를 살펴볼만하다.
- 두 부분 구간의 앞 부분의 첫 인덱스를 h, 뒷 부분의 첫 인덱스를 t 라고 했는데 당연히 t 가 더 커야한다. 그런데 사용자는 다양성의 집합체이기에 두 정수의 크기 비교에 어려움을 겪는 사람들이 있을 수 있다. h 가 더 크게 입력되었을 때는 뒤집어서 실행한다.
- 두 부분 구간이 겹치는 것은 이 함수에서는 용납이 안 된다. 그것을 제한다.
- 나머지 인덱스 에러도 고려할 수 있다. 가령 t-size 가 배열의 마지막 인덱스를 넘었다든지… 하지만 그것은 파이썬이 알아서 검사해줄 것이기 때문에 만들지 않았다.
이제 본격적으로 함수를 만들어보자.
def rotate(arr, n):
# 1.
if not arr:
return arr
N = len(arr)
n %= N
if not n:
return arr
def solve(lo, mid, hi):
# 2.
# lo는 왼쪽 구간의 첫 인덱스
# mid는 왼쪽 구간의 마지막 인덱스
# mid+1은 오른쪽 구간의 첫 인덱스
# hi는 오른쪽 구간의 마지막 인덱스
l_size = mid - lo + 1
r_size = hi - mid
# 3.
if l_size == r_size:
swap(arr, lo, mid+1, l_size)
return
# 4.
if l_size > r_size:
swap(arr, lo, mid+1, r_size)
solve(lo+r_size, mid, hi)
else:
swap(arr, lo, hi-l_size+1, l_size)
solve(lo, mid, hi-l_size)
# 5.
solve(0, N-n-1, N-1)
return arr
- 기본적인 확인을 한다.
- 배열이 비거나, 횟수가 0이면 그대로 반환한다. 이 부분은 모든 함수 공통이다.
- 분할정복해 나갈 함수를 정의한다.
- 이 분할정복 함수는 원하는 두 구간을 설명할 수 있어야 한다. 어떤 문제를 설명하기 위해 필요한 변수는 적으면 적을수록 좋다. 우리의 경우에는 함수의 대상이 되는 두 구간이 반드시 붙어있다는 것을 알 수 있는데 따라서 두 구간의 시작 인덱스와 왼쪽 구간의 마지막 인덱스만 있으면 세 가지 변수로 두 구간을 설명할 수 있다. 세 변수에 대한 설명은 함수 안에 주석으로 추가적으로 설명했다.
- 분할정복 함수의 기저사례를 정의한다.
- 분할정복은 그 특성상 재귀함수를 이용한다. 재귀함수를 사용할 때는 무한루프에 빠지지 않게 항상 기저사례를 정의하고 시작해야 한다. 우리의 solve 의 기저사례는 어떤 경우일까? 바로 두 구간의 크기가 같을 때다. 두 구간의 크기가 같다면 바로 구간을 교체하고 끝내면 된다. 보통의 경우 두 구간의 크기가 같지 않기 때문에 교체 후에 또 함수를 재실행하는 것이다.
- 함수를 분할한다.
- 두 구간으로 나눌 때 어떤 경우는 왼쪽의 크기가 클 수 있고, 다른 경우는 오른쪽의 크기가 클 수 있다. 이를 구분해줘야 한다. 길이가 큰 쪽을 짧은 쪽의 길이로 또다시 나눠 실행해야 하기 때문이다. 안의 인자가 헷갈릴 수 있다. 반드시 작은 입력으로 테스트해보기를 강력히 권장한다. 나도 이 부분에서 1시간은 헤맸다. 일단 내가 테스트했을 때는 돌아간다.
- 분할식을 실행한다.
- 처음 시작은 배열 전체를 대상으로 하고, 왼쪽 구간의 시작은 0, 왼쪽 구간의 끝은 ‘N-n-1’, 오른쪽 구간의 끝은 ‘N-1’이 된다. 마침내 정복된 배열을 반환한다.
동작은 잘 하는데 4번이 좀 어렵다. 유심히 살펴보자.
많은 분할정복 알고리즘의 경우 분할과 정복을 명확히 나눌 수 있다. 대표적인 분할정복 알고리즘의 예인 병합정렬을 보자. 많은 예제에서 분할하는 과정을 divide, 정복하는 과정을 merge 로 정의해 실행한다. 이 경우에도 그럴까?
정답은 ‘이 함수도 그렇다’이다. 분할정복 배열 회전 함수에서는 분할하는 함수는 solve, 정복하는 함수는 swap 이 된다. 전형적이고 아름다운 분할정복 알고리즘이라 할 수 있겠다.
이 함수가 많이 어렵다. 하지만 이해만 할 수 있다면 실력이 한꺼풀 성장할 수 있다고 믿는다. 다른 함수는 다 놓쳐도 분할정복 방법만큼은 작은 입력부터 손으로 써서 이해할 수 있도록 하자.
4. 마치며
결국 마쳤다. 시간이 꽤 걸렸는데 그래도 끝냈으니 홀가분하다. 다음엔 어떤 알고리즘을 해야할까? 이제 시작일 뿐이다.
포스트에서는 오른쪽으로 회전하는 것만 다뤘다. 완전한 코드가 되려면 왼쪽으로 회전하는 것도 같이 동작하도록 만들어야 한다. 이를 고민해보라. 어떤 함수의 경우에는 매우 간단하고, 어떤 함수의 경우에는 생각을 좀더 해야할 수도 있다.
이상 포스트를 마칩니다.
