최대 연속 부분수열 합을 구하는 4가지 알고리즘

최대 연속 부분수열 합을 구하는 4가지 알고리즘

2018, Dec 24    

목차

  1. 들어가며
  2. 문제 소개
  3. 알고리즘 소개
    • 3.1. 완전탐색: \(O(2^n)\)
    • 3.2. 부분합 수열: \(O(n^2)\)
    • 3.3. 분할정복: \(O(nlog_2n)\)
    • 3.4. 동적 계획법: \(O(n)\)
  4. 마치며

1. 들어가며

요즘 Codility에서 간간히 문제를 풀고 있다. ‘lessons’ 섹션을 하나씩 풀어나가고 있는데 생각보다 어려워서 깜짝 놀랐다. 이곳은 정답만 평가하는 것이 아니라 성능까지 테스트하는데, 문제를 풀 수 있는 최적의 알고리즘이 아니면 100점을 주지 않는다. 덕분에 의도치 않게 이상한 공부를 많이 하고 있다.

그중 하나로 며칠 전에 푼 MaxSliceSum 문제가 있다. 숫자 배열의 연속된 부분수열의 최대합을 구하는 문제인데 성능 30%, 100%, 0%을 오가는 다양한 알고리즘을 만졌다. 그래서 오늘은 이 문제를 해결하는 다양한 알고리즘들을 소개하려고 한다.

이 문제를 해결하는 최적의 방법은 동적 계획법인데, 난이도가 낮아 동적 계획법 훈련에 적합해서 그런지 관련된 포스트가 굉장히 많다. 백준 강의 유튜브 영상도 있고. 난 총 4가지, 완전탐색, 부분합 배열 이용, 분할정복, 동적 계획법 알고리즘을 소개할텐데 뒤로 갈수록 효율적이다. 하지만 이중 완전탐색은 내가 만들었기에 다른 곳에서 보기 쉽지 않다. 성능은 \(O(2^n)\)으로 최악이지만 재밌고 직관적이다. 참고해주면 좋겠다.

2. 문제 소개

이 문제는 비어 있지 않는 숫자 배열에서 합이 최대가 되는 연속된 부분수열 구간의 합(Largest sum of continuous subarray in a non-empty array)을 구하는 문제이다. 사진을 통해 이해하면 빠르다.

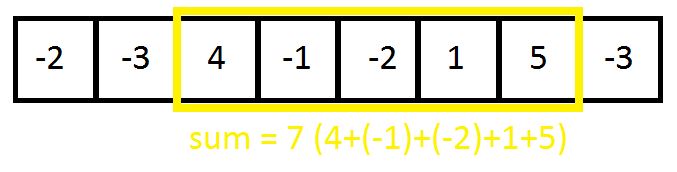
largest-subarray-sum

위 배열은 무난한 정수 배열이다. 배열에서 4부터 5까지 연속된 구간의 합은 7로 다른 어떤 부분 배열의 합을 구해도 7보다 크지 않다. 우리의 목표는 이렇게 7에 대응되는 연속된 부분수열의 합의 최대값을 구하는 것.

이 문제에서 수 배열은 정수배열이라고 가정한다. 또한 입력된 배열의 크기는 1 이상이며 빈 배열은 입력되지 않는다. Codility 문제에서는 정답의 범위를 \([-2^{31}, 2^{31}-1]\)로 한정했기 때문에 그대로 따르도록 하겠다.


4가지 함수를 모두 구현한 다음 각 함수를 테스트할 코드는 다음과 같다.

test_case = [[2],
             [-1],
             [-2, 1, -2],
             [1,2,3,4,5],
             [-3, -4, -5, -2, -1, 0],
             [3, 2, -6, 4, 0],
             [100, -100, 50, -50, 1000],
             [-1000, -1000, -1000, -1000],
             [1, 2, -1, 15, 0, 5, 1000, -1000],
             [-2, -3, 4, -1, -2, 1, 5, -3],
	     [-1, -2, -3],
            ]
ans = [1, 2, -1, 15, 0, 5, 1000, -1000, 1022, 7]
functions = [exhaustive_search, partial_sum,
             divide_conquer, dynamic_programming]


for func in functions:
    print('Function is', func.__name__)
    for i in range(len(test_case)):
        try:
            assert cumulative(test_case[i]) == ans[i]
        except:
            print('test_case is', test_case[i], 'and ans is', ans[i], \
                  '.. but i got', max_consecutive_sum(test_case[i]))

미리 테스트 케이스와 그의 답들을 준비해놓았다. 만든 함수를 배열에 담고 각각 순회하며 테스트 케이스에 적용한 결과와 답이 일치하지 않으면 뭔가 표준출력에 뱉어낼 예정이다.

함수를 다 만들고 실행해보도록 하자.

3. 알고리즘 소개

위에서 이야기한대로 소개할 알고리즘은 총 4개이다. 완전탐색, 부분합 배열 이용, 분할정복, 동적 계획법. 각각의 시간복잡도는 \(O(2^n), O(n^2), O(nlog_2n), O(n)\)이 된다.


3.1. 완전탐색: \(O(2^n)\)

언제나 문제를 그대로 풀기 보다는 보다 작은 부분문제로 나누고 이를 활용해 문제를 푸는 노력을 하는 것은 바람직하다. 나는 답을 만드는 과정을 다음과 같이 구성해도 된다고 생각했다. 일단 부분문제를 만들었다.


\[ \displaylines{ \text{f(now, tmp_ans):} \\ \textbf{현재 탐색할 인덱스가 now이고,} \\ \textbf{그 전까지 만든 최대값이 tmp_ans일 때,} \\ \textbf{배열의 끝에서의 최대 연속된 부분수열의 합} } \]


위 부분문제 함수는 배열의 인덱스를 0부터 시작해서 한 단계씩 나아가면서 지금까지 만든 중간값을 사용해 최종적인 답을 구할 것이다.

현재 인덱스가 now 이고, 지금까지 구한 중간합이 tmp_ans 라고 할 때 답을 구하면서 고려해야 할 모든 경우의 수는 총 4가지라고 생각했다.

  1. 배열의 현재 인덱스값 하나만 가지고 끝내는 경우(크기가 1인 부분수열의 합은 바로 자신이다.)
  2. 지금까지 구해온 답에 현재 배열의 now 인덱스 값을 더해서 끝내는 경우
  3. 지금까지 만든 값을 버리고 현재 인덱스 값을 가지고 다시 시작하는 경우
  4. 현재 값과 지금까지 만든 값을 포함해서 계속해서 답을 찾아나가는 경우


현재 인덱스에서 답을 찾을 수 있는 모든 경우의 수는 이 네 가지뿐이며 중복 또는 누락이 없다.(경우의 수에서 이 두 가지를 꼭 고려해야 한다.)

결국 이 4가지 값 중 최대의 값을 찾으면 그 인덱스에서의 최대값이 된다. 코드로 옮겨보자.

# 답의 하한선보다 작은 MIN 지정
MIN = -2 ** 31 - 1


def exhaustive_search(arr):
    N = len(arr)

    def find(now, tmp_ans):
        if now == N:
            return MIN

        ans = max(arr[now], # 1.
                  tmp_ans + arr[now], # 2.
                  find(now + 1, arr[now]), # 3.
                  find(now + 1, tmp_ans + arr[now])) # 4.
        return ans

    return find(0, 0)

코드의 중요한 부분을 살펴보면 다음과 같다.

  • 답의 하한을 정한다.
    • Codility에서 정한 답의 하한에서 1을 뺐다. 그러면 내가 만든 함수의 답은 그보다는 커질 것이다. 이는 다른 알고리즘 모두 동일하다.
  • 알고리즘의 핵심 재귀함수 find 를 정의한다.
    • 위 함수는 현재 인덱스 now, 지금까지 만든 중간값 tmp_ans 을 받는다.
    • 재귀함수의 탈출조건을 정한다. 0부터 시작해서 배열의 끝까지 가는데 now 가 배열의 크기에 다다랗다는 것은 끝에 도달했다는 것을 의미하기에 MIN을 반환해 함수를 끝낸다.
    • 4가지 경우의 수로 구한 답 중 최고값이 현재 now, tmp_ans 에서의 답이 된다.
    • 이때 두 find 를 눈여겨보자. 3번의 경우는 지금까지 만든 값을 버리고 다시 탐색을 시작하고, 4번의 경우는 이전값과 현재값을 포함해 계속 전진하다.
  • find(0, 0)으로 함수를 실행한다. 첫 인덱스는 당연히 0이고, 또 이제 시작이기에 만들고 있는 중간값이 없기 때문에 중간값도 0이다.


몇 가지 테스트해보라. 신기하게도 정말 잘 돌아간다. 시간 복잡도는 어떻게 될까? 한 번에 find 실행으로 두 번의 find가 이어진다. 배열의 크기가 커질수록 총 실행횟수가 2배씩 커지기 때문에 \(O(2^n)\).

Codility에 이 함수를 제출했는데 Performance(성능)가 0이 나온다. ㅋㅋ 그래도 이 코드, 아름답지 않나요?

3.2. 부분합 수열: \(O(n^2)\)

다음은 부분합(Partial sum) 수열을 통해 문제를 해결해보자. 부분합 수열은 인덱스 i 의 값에 원 수열 arr 의 0부터 i 인덱스까지의 합을 담은 수열이다.


\[ \displaylines{ \text{p_sum}: \textbf{arr의 부분합 수열} \\ \text{p_sum[i]} = \displaystyle\sum_{i=0}^{i} arr_i } \]


부분합 수열은 다양한 알고리즘을 해결하는 데 큰 도움이 되는데 그 중에서도 배열의 특정 구간의 합을 구하는 데에도 부분합 수열이 유용하다.

가령 어떤 수열의 [lo, hi] 구간의 합을 구하려고 할 때 다음 식을 이용하면 편하기 때문이다.


\[ \displaystyle\sum_{i=lo}^{hi} arr_i = \text{p_sum[hi] - p_sum[lo-1]} \]


p_sum[hi] - p_sum[lo-1]을 구하면 [lo, hi] 구간의 합을 구할 수 있다. 이때 뒷 부분이 ‘lo’가 아닌 ‘lo-1’이라는 것을 기억하자. lo 부분은 포함할 값이기 때문에 그전까지의 합만 빼줘야 닫힌 구간의 합을 구할 수 있다.

바로 이 식을 이용해서 수열의 모든 부분구간에 대해 구간합을 구하고 그중 최대값을 반환하면 되겠다.

부분합 개념만 가지고 있으면 코드 자체는 어렵지 않다. 바로 살펴보자.

def partial_sum(arr):
    # 1.
    arr = [0] + arr
    N = len(arr)
    p_sum = [0] * N
    ans = MIN

    # 2.
    for i in range(1, N):
        p_sum[i] = p_sum[i-1] + arr[i]

    # 3.
    for hi in range(1, N):
        for lo in range(1, hi+1):
            ans = max(ans, p_sum[hi] - p_sum[lo-1])

    return ans
  1. 원 배열의 앞에 ‘0’ 패딩을 하나 붙인다.
    • 이게 중요하다. 부분합을 사용할 때 자주 사용하게 되는 기교인데 이렇게 ‘0’을 붙이는 이유는 구간의 합을 구하는 위의 식과 관련이 있다. [lo, hi] 구간의 합을 구할 때 만약 구간이 [0, 3]이라고 하자. 위 식에서 빼는 부분이 ‘lo-1‘이기 때문에 인덱스가 ‘-1’이 되서 값이 이상해진다. 따라서 배열 앞에 ‘0’을 붙이고 인덱스를 1부터 시작하면 lo 가 0일 때도 문제없이 구할 수 있다.
  2. 부분합 배열 p_sum을 계산한다.
  3. 모든 부분수열의 합을 계산할 for 문을 중첩한다.
    • hi 는 1부터 배열의 끝까지 진행하되, lo 는 hi 까지만 진행한다.
    • 두 번째 for 문이 ‘hi+1‘까지인 것을 기억하자. 그래야 부분수열의 크기가 1일 때도 계산된다.


위 알고리즘의 시간복잡도는 for 문이 두 번 중첩되어 \(O(n^2)\)이 된다. 이 알고리즘은 내가 Codility에 처음 제출했던 알고리즘인데 성능이 30%에 안 나와서 깜짝 놀랐던 기억이 있다.

3.3. 분할정복: \(O(nlog_2n)\)

이 알고리즘이 분할정복으로도 가능할지 생각못했는데 어느 블로그에서 좋은 감명을 받았다. 아이디어를 주신 데 감사하다.


우리가 정답을 구할 구간의 인덱스의 최소값을 lo, 최대값을 hi라고 하자. 그리고 그 중간 인덱스는 mid이다. 이때 정답을 만드는 구간은 세 가지 중에 하나가 된다.

  1. [lo, mid], 즉 원 배열의 왼쪽 반에 있을 경우
  2. [mid+1, hi], 원 배열의 오른쪽 반에 있을 경우
  3. 그 외, 양쪽 절반에 걸쳐 있는 경우

이 세 가지 안에 정답이 반드시 있으며 중복되거나 놓친 부분은 없다.(이 결론이 매우 중요하다!)

따라서 원 배열을 절반으로 나눠 나가고(분할), 세 가지 경우에서 만들어지는 중간합 중 최대값을 선택하면(정복) 최종적으로 우리가 원하는 원 배열의 최대값을 구할 수 있다.

def divide_conquer(arr):
    N = len(arr)

    def find(lo, hi):
        # 1.
        if lo == hi:
            return arr[lo]

        mid = (lo + hi) // 2
	# 2.
        left = find(lo, mid)
        right = find(mid+1, hi)

        # 3.
        tmp = 0
        left_part = MIN
        for i in range(mid, lo-1, -1):
            tmp += arr[i]
            left_part = max(left_part, tmp)

        tmp = 0
        right_part = MIN
        for i in range(mid+1, hi+1):
            tmp += arr[i]
            right_part = max(right_part, tmp)

        # 4.
        return max(left, right, left_part + right_part)

    # 5.
    return find(0, N-1)
  1. 분할과 정복을 동시에 수행하는 find 함수를 정의한다.
    • 분할은 재귀를 거치지 때문에 탈출조건을 정해줘야 한다. 탈출조건은 배열을 절반씩 나눠나가면서 더 이상 나눌 수 없을 때, 즉 원소가 1개일 때이다. 이때 자신의 원소값을 반환한다.
  2. 두 경우의 수를 구한다.
    • 입력 받은 구간의 왼쪽 절반에 답이 존재하거나(left), 오른쪽 절반에 존재하거나.(right)
  3. 마지막으로 최대합이 두 구간에 걸쳐 있을 때의 답을 구한다.
    • [lo, mid] 구간의 최대합과 [mid+1, hi] 구간의 최대합을 구하면 걸쳐 있는 구간의 최대합이 나온다.
  4. 정답은 세 가지 경우의 수의 최대값이다.
  5. 함수를 시작한다. 원배열의 시작과 끝 인덱스를 넣고 답을 찾아나간다.

시간복잡도는 어떻게 되는가? 배열을 절반씩 나누기 때문에 기본적으로 \(log_2n\)인데 이렇게 나눌 때마다 \(n\)씩 답을 찾기 때문에 이를 곱해 \(nlog_2n\)이 된다.


분할정복을 많이 다뤄보지 않으면 헷갈린다. 하지만 분할정복의 정석이라고 할 수 있는 병합정렬의 동작방식만 이해할 수 있으면 충분히 이해할 수 있다.

3.4. 동적 계획법: \(O(n)\)

가장 정석적이고 바람직하며, 간단한 방법이다.

어떤 문제에 대해 해결가능한 더 작은 부분문제로 나눌 수 있다면 해결뿐 아니라 최적화가 가능해지는데, 이 문제에 대해 다음과 같은 부분문제를 만들 수 있다고 한다.


\[ \displaylines{ \text{배열 arr에 대해서,} \\ f(i) := \text{인덱스 i을 오른쪽 끝으로 갖는 구간의 최대합} } \]


이때 다음과 같은 식이 성립한다.


\[ f(i) = \begin{cases} max(0, f(i-1)) + arr[i] & \quad if \phantom{2} i > 0, \\ arr[i] & \quad if \phantom{2} i == 0 \end{cases} \]


이렇게 간단하다니. 몇 개 테스트해보라. 진짜로 성립한다. 이 식도 분할정복 식에서 참고한 분에게서 얻었다.

그렇다면 이제 할 일은 동적 계획법을 사용해서 0 인덱스에서부터 배열의 끝 인덱스까지 캐쉬를 채워나간 뒤 맨 캐시의 최대값을 반환하면 된다.

def dynamic_programming(arr):
    cache = [None] * len(arr)
    # 1.
    cache[0] = arr[0]

    # 2.
    for i in range(1, len(arr)):
        cache[i] = max(0, cache[i-1]) + arr[i]

    return max(cache)
  1. i 가 0일 때는 배열의 첫 값이 곧 캐쉬의 값이다.
  2. 그 외에는 식대로 값을 만들어 나간다.

이 동적 계획법은 위의 식이 성립한다는 것만 알면 끝이다. 그 다음은 코드로 옮기기만 하면 되기 때문이다. 시간복잡도는 길이 \(n\)의 캐쉬를 채워나가기 때문에 단순히 \(O(n)\)이 된다.

프로그래밍 세계에서 단순하면서 성능이 좋은 해결법을 ‘세련됐다’고 표현하는데 바로 이 식이 그렇다. 지금까지 방법들 중 코드도 제일 짧으면서 시간복잡도도 제일 우수하기 때문이다. 만약 코딩 테스트에서 이 문제를 만났고, 정답을 하나만 제출해야 한다면 반드시 이 방법을 제출해야 한다.(나도 그럴 생각이다)


자 이제, 맨 처음 만든 테스트 식을 모두 호출해보자. 만든 모든 함수에 대해 하나라도 답이 어긋나는 게 있으면 에러 메시지를 출력해야 하는데 모두 테스트를 통과한다. 우리가 만든 알고리즘들이 모두 정답은 낸다는 것을 알 수 있다.

4. 마치며

4가지 방법을 모두 살펴봤다. 문제 자체가 엄청 어렵진 않아서 네 가지 방법 중 이해하기 어려운 것은 사실 없다. 분할정복식은 병합정렬처럼 분할정복의 교과서 같이 일반적인 형태로 코드가 구현되며, 동적 계획법은 이렇게 쉬워도 되나 싶을 정도로 코드가 간단하다.

근데 난 첫 번째 알고리즘과 네 번째 알고리즘에서 큰 통찰을 느꼈다. 두 가지 경우 모두 원 문제에서 부분문제를 도출해냈다. 근데 난 첫 번째 부분문제를 완전탐색으로까지는 구현했는데 이를 승화해 동적 계획법으로까지 연결하는 데는 실패했다. 사실 그 작업을 하는 데 정말 많은 시간을 들였는데 결국 안 됐고 하루동안 좌절했었다. 그래서 성능을 개선하지 못했다. 반면에 네 번째 알고리즘은 매우 간단한 식으로 동적 계획법을 구현했다.

그래서 내가 느낀 교훈은, 같은 문제라도 부분문제를 어떻게 정의하느냐에 따라 개선 여부나 최종적인 성능의 차이에서 극적인 차이를 보일 수 있다는 것이다. 한 문제에 대해 더 좋은 부분문제를 정의할 수 있는 것이 곧 실력이다. 내가 더 정진해야 할 부분이기도 하다.

객관적으로 어렵지 않은 문제에서 시간을 꽤나 잡아먹혔고, 큰 통찰을 얻었다. 그래도 난 성장하고 있음을 확신한다. 다시 더 파고들어보자.

이상 포스트를 마칩니다.

Twitter Facebook Google+
# Algorithm # Max_slice_sum # Largest_continous_sum_in_subarray