피보나치 수열 알고리즘을 해결하는 5가지 방법
목차
- 들어가며
- 피보나치 수열이란?
- 알고리즘 소개
- 3.1. 기본 재귀적 풀이
- 3.2. 반복적 풀이
- 3.3. 동적 계획법을 사용한 풀이
- 3.3.1. 반복적 동적 계획법 풀이
- 3.3.2. 재귀적 동적 계획법 풀이
- 3.4. 행렬 곱셈을 활용한 풀이
- 3.5. 일반항 사용
- 마치며
- 자료 출처
1. 들어가며
오랜만에 알고리즘 포스트다. 오늘 포스트는 피보나치 수열 알고리즘을 해결하는 5가지 방법에 대해 살펴보고자 한다. 이 포스트는 해야지 해야지 하고 미루다 이제야 하게 되었다. 결국 하게 됐는데 사실 쉽지 않을 것 같다. 최소 6시간 정도 잡고 있는데 짬짬이 시간 내서 만들어야겠다. 언제나 말하지만, 한 문제를 해결하는 방법을 여러 개 알고 있는 것은 언제나 좋다. 그래야 행복하기 때문이다. 한 번 시작해봅시다.
2. 피보나치 수열이란?
피보나치 수열(Fibonacci Sequence)은 너무나 유명한 수열로 수학을 공부하지 않은 이들에게도 상식으로 통할 정도로 잘 알려져 있다. 피보나치는 12~13세기에 살았던 이탈리아 수학자로 토끼 번식에 대한 글을 쓰면서 피보나치 수열을 소개했다고 한다. 재밌게도 피보나치는 본명이 아니라고 하는데, 피보나치의 본명은 ‘Leonardo Pisano Bigollo’ 또는 ‘Leonardo Bonacci’라고 한다. 어떻게 읽어도 ‘피보나치’로 읽히지는 않는데, 그가 이 단어로 알려진 것은 후대 역사가가 그의 아들 이름 ‘Filius Bonacci’를 잘못 읽어 ‘피보나치’로 소개하면서 부터라고 한다. 피보나치는 피보나치 수열로 너무나 유명해졌지만 서양 세계에 현재 우리가 쓰는 아랍 숫자를 소개한 책인 ‘Liber Abaci’의 저자로도 알려져 있다고 한다.
피보나치 수열은 상당히 단순한 단조 증가(monotonically increasing) 수열로 0번째 항은 0, 1번째 항은 1, 그 외 항은 전번, 전전번 항의 합으로 표현된다.
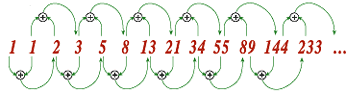
위 그림은 피보나치 수열의 첫 10항 정도를 보여주고 있다. 13, 21, 34, 55는 유명한 피보나치 수이다. 여기서 재밌는 것을 하나 발견할 수 있는데 1부터 10까지의 자연수의 합과 10번째 피보나치 수가 55로 같다.
우리가 해결하고자 하는 문제는, 0 이상의 정수 n 이 주어질 때 n 번째 피보나치 수를 구하는 것이다. n 번째 피보나치 수를 구하는 fibo 함수는 다음과 같이 정의할 수 있을 것이다.
\[ fibo(n) = \begin{cases} 0 & \quad \text{if } n \text{ is 0,} \\ 1 & \quad \text{if } n \text{ is 1,} \\ fibo(n-1) + fibo(n-2) & \quad \text{otherwise.} \end{cases} \]
이 기본 함수를 바탕으로 피보나치 수를 구하는 다양한 알고리즘을 살펴보자.
3. 알고리즘 소개
피보나치 수열은 재귀함수의 활용이나 동적 계획법을 연습하는 데 흔히 쓰인다. 그 방법들을 포함해 후에 조금 까다로운 방법까지 모두 살펴보도록 하자. 5가지 알고리즘을 소개하는데, 대체로 뒤로 갈수록 시간 복잡도가 낮아지는 풀이가 된다.
참고로, 여기서의 n 은 0 이상의 정수로 한정한다. 그래서 Input validation은 따로 하지 않겠다.
3.1. 기본 재귀적 풀이
가장 구현하기 쉬운 풀이가 그 정의에 충실한 재귀적 풀이이다. 앞서 우리는 n 번째 피보나치 수를 구하는 fibo 함수를 만들었다. 이를 그대로 구현하면 된다.
def fibo(n):
return fibo(n-1) + fibo(n-2) if n >= 2 else n
for n in range(1, 11):
print(n, fibo(n))
워낙 간단한 로직이라 삼항 연산자 한 줄로 깔끔하게 구현됐다. n 이 0이나 1일 때는 값도 0, 1이기 때문에 그대로 반환하면 되고, 2 이상일 때만 재귀 함수 두개로 분기해 값을 반환한다.
시간 복잡도는 함수가 한 번 호출되면 다시 두 번 호출되기 때문에 지수적으로 증가해 O(\(2^n\))이 된다.
3.2. 반복적 풀이
위의 그림을 다시 보자. 가령 내가 10번째 피보나치 수를 찾고 싶다면 0번째(0), 첫 번째(1) 피보나치 수부터 계속 반복적으로 더해서 앞으로 한 발씩 전진하며 최종적으로 10번째에 도달할 수 있다. 그러니까, 피보나치 알고리즘을 재귀적으로도 풀 수 있지만 for 를 활용한 반복문을 통해서도 해결할 수 있는 여지가 있다.
def fibo(n):
if n < 2:
return n
a, b = 0, 1
for i in range(n-1):
a, b = b, a + b
return b
for n in range(1, 11):
print(n, fibo(n))
n 이 2 미만일 때는 아까와 같이 그대로 반환한다. 그 다음이 재밌는데 n 이 2 이상일 때는 n-1 번만큼 반복문을 시행한다. 그 이유는 우리가 0번째 값 a 와 첫 번째 값 b 를 계속 반복하면서 원하는 값을 만들텐데, n 이 2일 때는 단 한 번(n-1)만 계산하면 원하는 값을 만들 수 있기 때문이다.
그리고 한 번의 반복마다 ‘a, b = b, a + b’를 시행한다. 파이썬에서 이와 같이 대입을 사용하면, ‘a = b’, ‘b = a + b’와 같이 대입이 이루어지는데 이는 파이썬의 packing & unpacking과 관련이 있다. 새로 만든 b 에 이전의 a, b 값을 더해 새로운 피보나치 값을 만들어 나간다. 반복문이 끝나면 b 가 우리가 고대하던 n 번째 피보나치 수가 되며 이를 반환하면 된다.
앞선 재귀에 비해 매우 효율적인 방법이며 시간 복잡도는 O(n)이 된다.
참고로 이 코드는 Python 공식 홈페이지의 피보나치 함수를 조금 수정했다.
3.3. 동적 계획법을 사용한 풀이
앞서 말했듯, 피보나치 수 알고리즘은 동적 계획법을 연습하는 예제로 자주 쓰인다. 피보나치 알고리즘에서 동적 계획법이 쓰이는 이유는 기본적인 피보나치 수 알고리즘이 너무나 비효율적이기 때문이다. 우리가 첫 번째로 작성한 재귀적 알고리즘을 살펴보자. 일단 이 식은 매우 간단하고 기본 정의에 충실하다는 장점이 있지만 효율은 극악을 달리는데, 작성한 함수를 통해 100번째 피보나치 수를 구해보자. 아마 일반적인 컴퓨터로는 우리에게 긍정적인 시간 내로는 답이 나오지 않을 것이다. 그 이유는 피보나치 수열의 재귀적 특성에 있다.
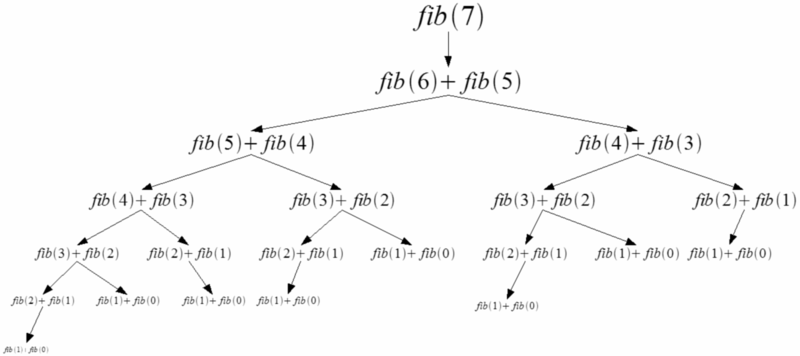
위 그림은 7번째 피보나치 수를 구할 때의 값을 구하는 과정을 표현하고 있다. 7번째 값을 구하기 위해서는 5, 6번째 값을 구해야 한다. 그 둘을 더해야 하기 때문이다. 알고리즘에서는 이와 같이 원 문제를 해결하기 위해 원 문제보다 작은 5, 6번째 같은 값을 구하는 것을 ‘부분문제(subproblem)를 푼다’고 한다. 이 부분문제를 풀기 위해 우리는 함수의 재귀 호출을 사용했다.
문제는 이 부분문제들이 fib(0), fib(1) 를 만나기 전까지 계속 쪼개지며 너무나 많이 등장한다는 것이다. 정확히는 부분문제가 많은 것보다도 부분문제가 중복(overlapping subproblems)된다는 것이 문제다. 그림에서 7번째 값을 구하기 위해 fib(3) 이 얼마나 많이 등장하는가? 직접 세보니 5번이나 등장한다. 이는 n 이 커질수록 기하급수적으로 커지는데 그래서 아까 100번째 값을 구해야 할 때 프로세스가 멈춘 것이다. 아까 재귀적 풀이의 시간 복잡도가 \(O(2^n)\)이라고 말했는데 n 이 100만 되어도 10진수로 대략 30자리 수다. 이는 조에 조를 곱하고 거기에 백만을 곱해야 하는 큰 수이다(12+12+6). 무진장이라는 단어가 부처의 다함 없는 자비로움을 표현하는 불교 용어라고 하는데, 바로 이런 수가 무진장 큰 수가 아니면 무엇이란 말인가?
그러면 이를 조금만 영리하게 풀어보자. 지금 문제가 부분문제가 너무 많이 중복되는 것이 문제라면, 각 부분문제를 해결할 때마다 그것을 저장하고 필요할 때마다 가져다 쓰면 되는 것이 아닌가? 예를 들면, 아까 7번째 피보나치 수를 구하기 위해서 3번째 피보나치 수 부분문제를 5번 해결한다고 했는데, 애초에 처음 구했을 때, 그것을 어딘가에 저장해둔다면 그 값이 또 필요할 때 반복계산할 이유가 사라진다. 동적 계획법이 쓰일 이유가 충분하다!
동적 계획법 풀이에서는 부분문제들을 해결할 때마다 값을 저장하는 캐시를 만든다. 이런 동적 계획법 문제를 풀 때 해결할 수 있는 방법이 크게 반복문을 사용하는 반복적 풀이(iterative)와 재귀적 풀이(recursive)가 있는데 둘 다 살펴보자. 먼저 반복문을 활용한 반복적 풀이로 풀어보자.
3.3.1. 반복적 동적 계획법 풀이
부분문제의 답을 계산할 캐시의 형태나 타입은 문제의 특성에 따라 다양하게 설정할 수 있는데, 이렇게 쉬운 문제에서는 n 번째 피보나치 수를 n 인덱스에 저장하는 1차원 배열이면 충분해 보인다. 거의 모든 언어에서 통용될 수 있을 법한 풀이로 풀어보자.
# n을 100이라고 하자.
cache = [0 for _ in range(100+1)]
cache[1] = 1
for i in range(2, 100+1):
cache[i] = cache[i-1] + cache[i-2]
>>> print(cache[100])
354224848179261915075
아까와 달리 1초도 안 돼서 답이 나온다. cache 의 크기를 100이 아닌 100+1로 한 것은 크기를 100으로 하면 캐시의 마지막 인덱스가 99가 되기 때문이다. 그래서 1을 키워주어서 우리가 원하는 100번째 값을 저장할 수 있도록 한다.
부분문제의 값을 저장하고 그 부분문제를 해결해 나가며 최종적으로 답을 구한다. 사실 저 풀이는 아까 봤던 반복적 풀이와 원리적으로 같다. 둘을 굳이 분류한 것은 아까처럼 두 변수를 반복할 수 있는 것은 피보나치 알고리즘의 특수한 특성일 뿐이며 지금처럼 푸는 것이 동적 계획법의 정석이기 때문이다.
그리고 사실 위의 풀이는 참 더러운 코드다. cache 가 전역 공간을 낭비하고 있으며, 이 알고리즘을 사용할 유저에게 제시하는 인터페이스가 너무 구린 상태다. 이 두 문제를 해결하기 위해 코드를 함수로 감싸자.
def fibo(n):
if n < 2:
return n
cache = [0 for _ in range(n+1)]
cache[1] = 1
for i in range(2, 100+1):
cache[i] = cache[i-1] + cache[i-2]
return cache[n]
>>> print(fibo(100))
354224848179261915075
코드를 fibo 라는 이름의 함수로 감쌌다. 그래서 아까는 원하는 값을 구하기 위해 10줄 가까이를 복붙해 실행해야 했다면 이제는 함수에 인자 하나만 넘겨 실행하면 끝이다. 즉, 유저 인터페이스가 매우 간결해졌다. 기능이 모듈화되어 재사용성도 향상됐다. 또 전역 공간을 낭비하지 않는다. 캐시가 함수가 끝날 때마다 삭제된다.
이때 눈여겨 볼 점은 n 이 2보다 작을 때는 그 값을 바로 반환하도록 하는 것인데 이것을 안 하면 n 에 0이 들어왔을 때 ‘cache[1] = 1’에서 인덱스 에러가 발생한다.
3.3.2. 재귀적 동적 계획법 풀이
반복적 동적 계획법 풀이도 훌륭하지만, 재귀 함수를 사용하는 동적 계획법 풀이도 존재한다. 앞서 기본 재귀적 풀이의 비효율성을 언급하면서 ‘동적 계획법을 도입해 첫 부분문제를 해결하고 다시 필요할 때마다 가져다 쓰자’고 했는데 그 느낌을 살리기에는 이 방법이 더 괜찮다.
앞의 이 방법은 재귀적 풀이와 비슷하다. 차이가 있다면 캐시를 만들고, 그 캐시에서 부분문제의 답을 찾고 없으면 직접 계산한다는 정도이다. 먼저 많은 언어에서 통용될 법한 방법으로 코드를 짜보자.
def fibo(n):
cache = [-1 for _ in range(n+1)]
def iterate(n):
# 기저사례 1.
if i < 2:
return i
# 기저사례 2.
if cache[n] != -1:
return cache[n]
# 기저사례 충족 못할 시 값을 실제로 구함
cache[n] = iterate(n-1) + iterate(n-2)
return cache[n]
return iterate(n)
for n in range(1, 11):
print(n, fibo(n))
함수를 재귀적으로 풀 때 언제나 염두에 두어야 할 것은 함수가 더 이상 재귀 호출하지 않고 끝날 조건을 설정해줘야 하는 것이다. 그렇지 않으면 함수 스택이 넘치게 된다. 재귀 함수가 끝나도록 하는 조건을 기저사례(base case)라고 하는데, 단어가 딱딱해서 나는 그냥 내 마음대로 ‘탈출조건’이라고 부르기도 한다.
피보나치 알고리즘에서 기저사례는 n이 2 미만일 때다.(n은 0 이상의 정수로 이미 한정했다) 그리고 우리의 알고리즘에서는 기저사례가 하나 더 추가되는데, 그것은 원하는 부분문제를 이미 해결했을 때이다. 5번째 피보나치 수를 구하는 부분문제를 해결했다면, 다시 그 수가 필요할 때 그대로 가져다 쓰면 된다. 위 함수에서는 기저사례 2.에 해당한다.
난 캐시의 모든 인덱스를 ‘-1’로 초기화했다. 꼭 ‘-1’일 필요는 없는데, 모든 피보나치 수는 0 이상의 정수이기 때문에 캐시 값이 ‘-1’이라는 것은 n 번째 피보나치 수를 아직 계산 안 했다는 것이 된다. 캐시의 n 번째 인덱스의 값이 ‘-1’이 아니면 n 번째 피보나치 수를 구하는 부분문제를 이미 해결다는 뜻이기에 그대로 값을 반환한다.
두 기저사례를 하나라도 만족하지 못하면 재귀함수를 호출해 값을 구한다. 이때, 새로 구한 n 번째 값을 캐시에 저장함으로써 향후 이 값이 필요할 때 다시 사용한다.
많은 동적 계획법 문제의 경우, 소개한 재귀적, 반복적 동적 계획법을 모두 사용할 수 있다. 무엇을 쓸지는 취향의 문제인데 난 재귀적 동적 계획법을 선호한다. 그 이유는 재귀적인 방법이 현실의 큐에 익숙한 우리에게 상대적으로 반직관적이며 그 동작을 따라가보는 재미가 있기 때문이다. 다만 재귀적인 방법은 함수를 계속 호출하는 데 따르는 오버헤드가 발생하기 때문에 절대적으로는 반복적 동적 계획법 풀이에 비해 시간이 오래 걸린다. 그렇지만 둘 다 시간 복잡도는 \(O(n)\)으로 효율에 있어 극적인 차이가 발생할 정도로 비효율적이지는 않으니(우리가 \(BigO\) 표기법에서 상수를 무시하는 것과 같은 이치다) 너무 걱정하지 않아도 된다.
마지막으로, 파이썬 함수의 동작방식을 활용한 방법을 사용해 문제를 풀어보자.
def fibo(n, __cache={0: 0, 1: 1}):
"""Get nth fibonacci number"""
if n in __cache:
return __cache[n]
__cache[n] = fibo(n-1) + fibo(n-2)
return __cache[n]
fibo(100)
코드 동작 방식은 일반적인 재귀적 동적 계획법 방법과 같다. 여기서 눈여겨 볼 것은 ‘__cache’ 변수이다. 파이썬의 기본 자료구조인 dict 를 사용했는데 dict 는 배열에 비해 자료구조의 크기가 유동적으로 커질 수 있다는 장점이 있기에 dict 를 사용했다. 그보다도 더 의미가 있는 것은 캐시 자료구조가 함수 내부가 아닌 정의부에 선언되었다는 것이다.
일반적으로 함수 안에 선언한 데이터는 함수가 호출될 때 생성되며 함수가 종료될 때 폐기되고 자원이 회수된다. 그런데 위와 같이 원하는 데이터를 함수 정의부에 적으면 그 자료구조는 함수가 정의될 때 생성되어 함수가 호출될 때나, 종료될 때나 상관없이 함수 자체가 메모리에서 지워지기 전까지는 값이 유지된다. 우리의 함수에서는 실행 시에 캐시에 변화를 가하는데, 그 변화까지도 유지된다.
함수 정의 시에 ‘__cache’를 미리 선언했기 때문에, 함수 실행 시에는 n 만 인자로 넘기면 된다. 그것을 알리기 위해서 캐시 이름 앞에 ‘__‘를 불였다. 알다시피 파이썬에서 변수명을 정할 때 ‘_‘와 ‘__‘를 붙이는 것은 특별한 의미가 있는데, 그 중에서도 ‘__‘는 미약한 ‘private’의 의미로 ‘이 값은 사용자가 건드리지 말라’는 의미를 함축한다. 실제로 여기서는 캐시를 건드릴 이유가 없고 건드려서도 안 된다.
위와 같이 쓰는 것은 상당한 주의를 요한다. 함수 실행 시에 캐시가 꾸준히 변화하고 그 값이 보존되기에 함수가 계속 실행되면서 예기치 못한 에러를 맞닥뜨릴 수도 있기 때문이다. 조심해야 하지만, 이 함수를 써야할 때는 크게 문제가 없다. 파이썬의 내부 동작방식을 활용하기 때문에 파이썬에서만 구현할 수 있는 방식이다.
이 방법을 쓸 때는 몇 가지 단점이 있는데, 먼저 다른 언어 사용자들에게 가독성이 떨어질 수 있으며, 사랑받는 프로그램이 되기 위한 필수적인 조건인 프로그램의 설명문서가 비대진다는 것이다. 위의 저 100번째 값을 구하는 코드를 실행한뒤 ‘help(fibo)’를 실행해보면 그 의미를 알 수 있다.
이상 동적 계획법을 통한 피보나치 수를 구하는 알고리즘을 살펴보았다.
3.4. 행렬 곱셈을 활용한 풀이
행렬의 곱셈을 활용한 알고리즘이다. 사실상 이 포스트를 작성한 이유이기도 하며 백준 온라인 저지의 피보나치 문제에서 이 방법을 알게 되었다.
이 절에서는 n 번째 피보나치 수를 \(F{n}\)라고 하자.
이때, 피보나치 수들을 행렬화할 수 있는데, 이런 정리를 이끌어낼 수 있다.
\[ \begin{pmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n \]
이를 유도하는 과정은 여기를 참고하자. 이 포스트에서는 이 식이 맞다고 가정하고 계속 진행한다.
이 식을 통하면 오른쪽 행렬을 n 번 제곱하면 나오는 행렬의 [0, 1] 또는 [1, 0] 값이 \(F{n}\)이 된다. 즉 우리는 행렬 곱셈을 통해 피보나치 수를 구할 것이다.
그러면 제곱수를 구해야 하는데 논의를 더 진행시키기 전에 생각해보자.
가령 계산을 통해 \(2^{64}\)를 구해야 한다면 어떻게 구하는 것이 최선일까? 이 알고리즘을 공부하기 전에는 나는 ‘2를 64번 곱한다’고 실제로 답했는데 이보다 우아한 방법이 있다. 이는 \(2^1\)을 제곱하고 그 결과물인 \(2^2\)를 제곱, 또 그 결과를 제곱, …, 해서 \(2^{64}\)까지 만드는 것이다. 2의 1승부터 계산하면 6번의 계산이 나오는데 이는 \(log_264\)과 일치한다. 즉, 이 방법을 통하면 2의 \(n\) 승을 구하는데 \(O(log_2n)\)의 시간으로 끝낼 수 있을 것이고 우리의 행렬식도 같은 방법으로 제곱해 나가면 이전의 방법들의 \(O(n)\)을 획기적으로 개선할 수 있다.
이런 질문을 할 수 있다. ‘n 이 2의 제곱수이라면 참 좋겠지만 100과 같이 2의 제곱수가 아니면 어떻게 해야 하는가??’ 예를 들어 \(2^{100}\)을 2의 제곱수를 사용해 어떻게 구하면 될까? 당연한 말이지만 모든 자연수는 2의 제곱수의 합으로 표현할 수 있다. 100은 4, 32, 64의 합이고 그렇다면 \(2^{4}\), \(2^{32}\), \(2^{64}\)를 구해 이 셋을 곱하면 2의 100승을 만들 수 있다. 복잡도는 여전히 \((log_2n)\)이다. 이 방법을 통해 주어진 행렬의 n 승을 만들어내서 결과 행렬의 [1, 0]을 반환하는 함수를 만들자.
문제를 풀자. 이 함수는 앞선 함수들에 비해 조금 복잡하기 때문에 문제를 조금 더 작게 만들어 정복하자.
- 두 행렬을 곱하는 기능 : 우리 문제에서는 2 X 2 크기의 정방 행렬을 사용하는데 두 개의 행렬을 곱하는 기능을 만든다.
- 실제로 곱하는 기능 : 주어진 n 에 대해 기본 행렬을 n 번 곱한 행렬을 완성하는 기능을 만든다.
def fibo(n):
SIZE = 2
ZERO = [[1, 0], [0, 1]] # 행렬의 항등원
BASE = [[1, 1], [1, 0]] # 곱셈을 시작해 나갈 기본 행렬
# 두 행렬의 곱을 구한다
def square_matrix_mul(a, b, size=SIZE):
new = [[0 for _ in range(size)] for _ in range(size)]
for i in range(size):
for j in range(size):
for k in range(size):
new[i][j] += a[i][k] * b[k][j]
return new
# 기본 행렬을 n번 곱한 행렬을 만든다
def get_nth(n):
matrix = ZERO.copy()
k = 0
tmp = BASE.copy()
while 2 ** k <= n:
if n & (1 << k) != 0:
matrix = square_matrix_mul(matrix, tmp)
k += 1
tmp = square_matrix_mul(tmp, tmp)
return matrix
return get_nth(n)[1][0]
fibo(100)
행렬의 곱셈을 이용해 피보나치 알고리즘을 구현했다. 각 부분에 대한 설명은 아래와 같다.
- 먼저 변수 선언
- n 에 0이 들어올 경우를 위한 ZERO 항등원을 만든다. 위 값은 실제로 행렬의 항등원으로 n 이 0일 때는 [1, 0] 인덱스 값이 0이 된다. BASE 행렬은 우리가 곱해 나갈 기본 행렬이 된다. 앞선 정리의 오른쪽이 되는 행렬이다. 이를 n 번 곱하는 것이 우리의 목적이고 2의 제곱수를 활용해 구한다. 이때 이들은 수정을 가하지 않을 상수 취급하기 위해 변수명을 대문자화했다.
- 두 행렬을 곱하는 함수 square_matrix_mul 구현
- 인자로 받은 두 행렬을 곱하는 함수를 만든다. 이 알고리즘은 너비, 길이가 같은 정방형 행렬(square matrix)만 취급하기 때문에 코드가 단순하다. 대신 이름에 이를 꼭 명시해줘야 한다.
- 실제로 BASE 행렬의 n 승을 구하는 함수를 구현
- 행렬 피보나치 알고리즘에서는 이 함수만 이해하면 된다. 먼저 최종 결과물인 matrix 행렬을 만든다. n 이 0일 경우를 대비해 ZERO 가 되어야 한다. k 는 2의 k 승을 계산할 때 쓰인다. 0부터 시작해서 값을 키워나가며 n 이 \(2^k\) 승을 포함하는지(가령, 100이 16, 32, 64 등을 포함하는지)를 확인할 것이다. tmp 는 k 가 커짐에 따라 BASE 를 \(2^k\) 번 곱한 값을 저장해 나간다. n 을 구성하는 \(2^k\)마다에서 matrix 변수에 자신을 곱해나가며 matrix 를 키울 것이다.
- while 반복문을 통해 주어진 n 이 1, 2, 4, 8, … 등을 포함하는지 계산한다. 무한루프에 빠지지 않게 조건을 주어야 하는데 \(2^k\)가 n 이하일 때까지만 계산한다. 100은 \(2^6\) 보다는 크기 때문에 이를 포함할 수 있지만 자신보다 큰 제곱수는(\(2^7\) 이상) 상식적으로 포함할 수 없다.
- 0 이상의 정수 k 에 대해 자연수 n 이 \(2^k\)를 포함하는지 어떻게 확인할까? 비트 연산이 적절해 보인다. 100은 이진수로 \(1100100_{(2)}\)이고, 이때 1이 되는 자리수들이 100을 구성하는 4, 32, 64가 된다. 100에 k 를 0에서 1씩 키워 나가 AND 연산을 하면 100이 \(2^k\)를 포함할 때는 1, 아닐 때는 0을 반환할 것이다.
- 이 원리를 바탕으로 matrix 를 곱해 나간다. n 을 2진수로 변환했을 때 k 번째 자리수가 1로 채워져 있다면(‘n & (1 <<k) != 0’) matrix 에 tmp 를 곱하고, 아니면 이번 k 에서는 건너 뛴다. 이번 k 일 때 n 이 \(2^k\)를 포함하는 여부와 상관없이 while 문을 벗어나기 전까지는 k 는 1씩 증가시키고, tmp 는 자신을 곱해 \(2^k\)번째 행렬을 꾸준히 만든다. 100이 8, 16을 포함하지 않다가 32를 포함한 것과 마찬가지로.
코드 자체는 그리 길지 않다. 코드보다 내 설명이 더 길어진 것 같은데 설명이 잘 됐는지는 모르겠다. 어쨌든 행렬을 사용한 방법은 시간 복잡도가 \(O(log_2n)\)이기 때문에 위의 방법들보다 효율적이다. n 이 2의 64승쯤되는 압도적으로 큰 수에서는 그 효율을 실감할 수 있을 것이다.
이제 마지막 방법으로 넘어가자.
3.5. 일반항 사용
마지막으로 n 번째 피보나치 수를 구하는 일반항이 있다.
\[ a_{n} = \frac{1}{\sqrt{5}}\left(\left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n\right) \]
피보나치 수열의 일반항이 있다는 것이 신기했는데, 유도 방법은 밑의 2번째 출처에서 확인할 수 있다. 일단 진짜로 값이 나오는지 확인부터 하자.
def fibo(n):
sqrt_5 = 5 ** (1/2)
ans = 1 / sqrt_5 * ( ((1 + sqrt_5) / 2) ** n - ((1 - sqrt_5) / 2) ** n )
return int(ans)
fibo(100)
답이 나온다. 이게 무슨 알고리즘이냐고 물을 수 있지만, 알고리즘이 ‘문제를 해결하는 일련의 절차나 방법’이라는 것을 감안할 때 이 정의에 딱 부합한다.
시간복잡도는 위 식의 각 부분을 살펴봐야 하는데 제곱을 구하는 부분이 행렬 알고리즘에서 살펴본 것처럼 \(O(logn)\)이기 때문에 전체적으로 \(O(logn)\)이 된다. 행렬식과 같다.
4. 마치며
포스트를 마무리했다. 거의 몇 주간을 마음의 숙제로 남겨두고 있었는데 이제 좀 위안이 된다. 이제 마음 한구석의 찜찜함을 느끼지 않아도 될 것 같다.
알고리즘 포스트는 다른 카테고리 포스트에 비해 특히 더 에너지를 많이 쓰는 것 같은데, 그만큼의 가치가 있었으면 좋겠다. 내 능력에 달려있으니 더 노력해야 할 뿐이다.
다음 알고리즘 포스트는 1차원 벡터의 회전에 대해 다룬다. 가령 [1, 2, 3, 4, 5]라는 벡터에 대해 왼쪽으로 2만큼 회전하면 [3, 4, 5, 1, 2]가 되는데 이를 구하는 알고리즘을 4가지 정도 살펴보자.
5. 자료 출처
- 10 things you never know about FIBONACCI
- 피보나치 수 일반항
- 『알고리즘 문제 해결 전략』, 구종만, 인사이트(insight)
- 『파이썬 코딩의 기술』, 브렛 슬라킨, 길벗
