그래프와 트리의 관계에 대한 고찰
들어가며
학교에서 알고리즘 수업을 들을 때 빠지지 않는 자료구조가 있다. 그중 오늘 다룰 자료구조는 트리와 그래프인데, 워낙 중요해서 비전공자 대상 수업에서도 이 둘은 반드시 배우는 걸로 안다. 내가 배웠기 때문이다. 각종 테스트나 입사 면접 문제로도 자주 출제된다.
하지만 이 친구들이 중요한 것은 사실 ‘시험에 나오기 때문에’는 아니다. 중요하니까 많이 출제되는 것이지.
트리와 그래프가 중요한 진짜 이유는 이 둘이 현실의 대다수 또는 모든 것을 표현하는 개념이기 때문이다. 트리와 그래프는 서로 다르지만 깊은 관계가 있으며 나는 최근 이 둘의 관계에 대해 고민했었다. 그리고 어느 정도 결론을 내렸기 때문에 이에 대해 정리해보도록 하자.
그래프와 트리의 관계

그래프는 개체간의 “관계”를 다룬다. 현실에서 수많은 개체가 상호작용하는데 이 둘이 (정의하기 나름인) 관계로 연결되어 있을 때 이 개체의 노드를 엣지로 이을 수 있고 이것이 곧 그래프다.
그래프는 오일러가 그 유명한 “다리” 문제를 연구한 이래로 수많은 연구가 진행되었고 그래프의 형태에 따라 수많은 분류가 있다. 가령 엣지의 방향의 유무에 따른 분류, 엣지의 가중치의 유무에 따른 분류, 사이클 유무 등.
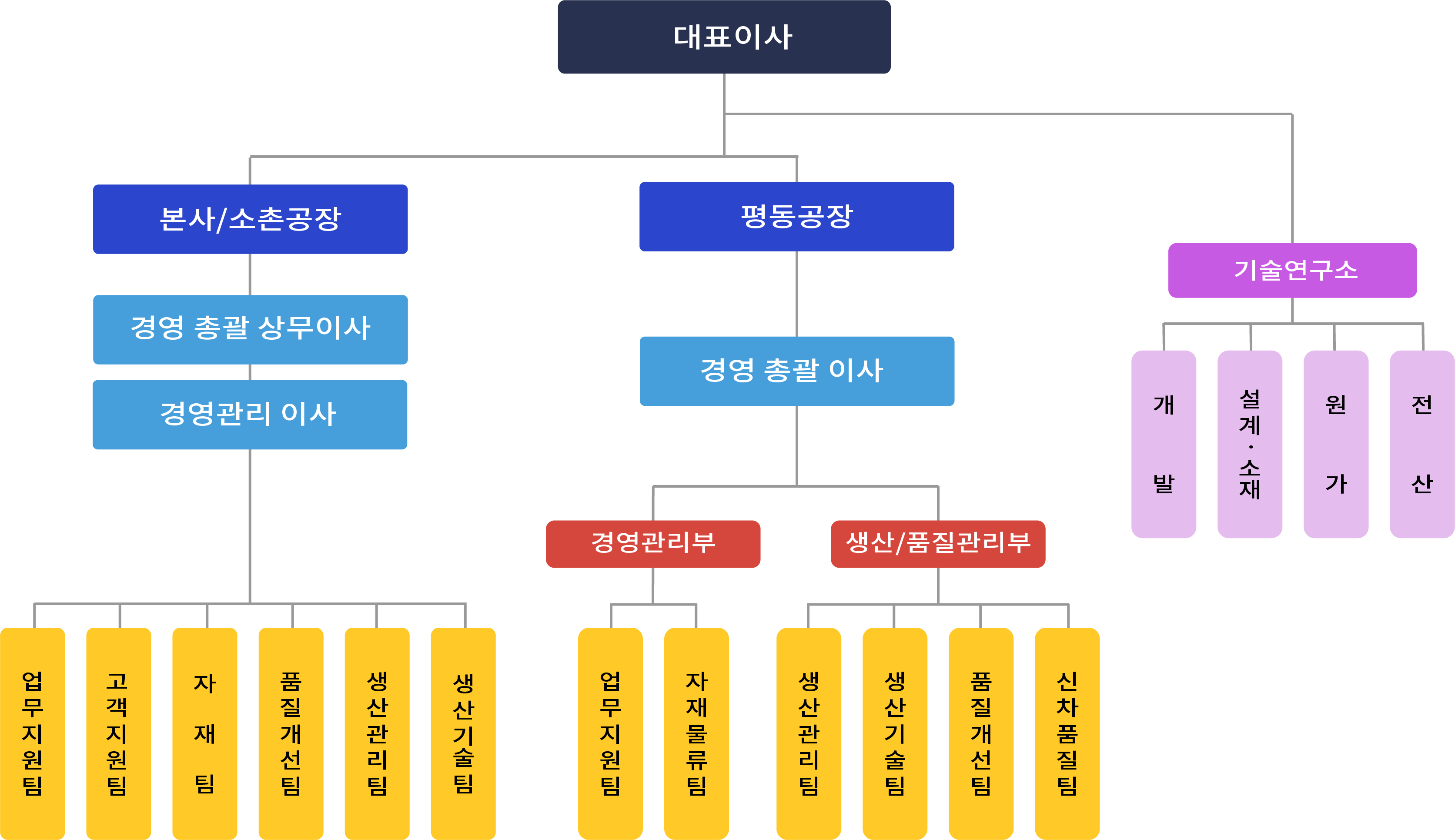
트리는 현실의 “계층”을 표현한다. 위 사진의 조직도가 대표적인데 정점인 대표이사부터 시작해서 자잘한 부서로 갈라져 나오는 것을 볼 수 있다. 트리는 그것을 추상화해 정점인 루트노드부터 시작해서 말단인 잎 노드까지 분기한다.
그래프와 트리는 분명 관계가 있어 보인다. 왜냐하면 트리도 부모노드와 자식노드가 계층관계로 이어져 있는 것 또한 “관계”라고 할 수 있기 때문이다.
그래서 난 처음에 트리와 그래프의 관계를 다음과 같이 도식화할 수 있다고 생각했다.
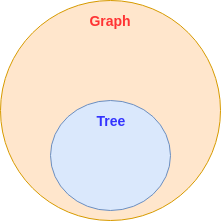
이 속에서 단순히 트리는 곧 그래프다. 이 특별한 그래프의 특징은 다음과 같다.
- 가중치가 없다.
- 사이클이 없다.
- 두 정점간 최단 경로가 단 하나뿐이다.
- 간선의 개수는 정점의 개수에서 1을 뺀 값이다.
수학자들이 연구한 수많은 그래프가 있는데 그중에서 트리는 “계층”을 표현하기 때문에 매우 중요하고 그래서 따로 이름까지 붙여 연구하는 것으로만 생각했다.
하지만 좀더 생각해보니 이게 다가 아니었다. 물론 트리는 관계를 표현한다. 하지만 트리는 그 이상이다. “계층”을 표현하기 때문이다. 트리에서는 정점과 말단을 구분하며 이는 현실의 수많은 조직을 대변한다. 사장과 말단이 같은 위치에 서는 것을 즐기는 회사는 별로 없으리라고 생각한다.
하지만 그래프는 개체간의 관계만 규정하지 그들의 계층관계까지 고려하지는 않는다. 그래서 실제로 위에서 언급한 트리의 특징을 모두 보이지만 루트노드가 딱히 정해지지 없는 그래프를, 다시 말해 계층 관계가 없는 그래프를 “루트 없는 트리(unrooted tree)”라고 정의하고 있다.
그래서 위의 사진처럼 그래프와 트리의 관계를 단순히 두 집합으로만 표현하면 안 된다. 트리는 그래프와 현실의 “계층”이라는 개념집합과의 교집합으로 보는 것이 타당하다.
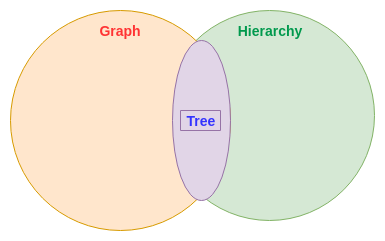
이 시선은 아까와 분명한 차이가 있다.
확실히 트리는 그래프에 속하기에 관계를 표현한다. 하지만 “계층”이라는 개념에까지 발을 담갔기 때문에 일반 그래프와 달리 계층을 표현할 수 있는 것이다.
마치며
트리와 그래프의 관계에 대해 고찰해봤다. 트리와 그래프의 관계를 ‘트리는 그래프와 계층 개념의 교집합’이라고 보는 시선을 가지고 이를 클래스 상속으로 표현할 수 있다고 생각했다. 충분히 가능할 것 같은데? 만약 Tree 클래스를 Graph 클래스와 HierarchyMixin 클래스의 상속으로 표현한다면 내 가정에 대한 구성적 증명이 되려나? 모르겠다.
이상 포스트를 마칩니다.
